因为没有预习的习惯，所以上课后发现竟然是数值计算便十分激动，以至于晚上又翘了一门课，迫不及待的想尝试能不能把轮子造出来。
虽然第四章没有什么代码，但是思路说的非常清晰。单站在复刻的角度上还是十分容易的。这次的轮子是建立在二维正方形矩形平板稳态导热问题，为了验证正确性选择传热学第五版P158页例题4-2的数据以验证答案的准确性。同时还使用了comsol进行对照。
忽略在实际开始前从另一道例题对照尝试通过高斯-赛德尔迭代法求解任意方程组的过程。在无内热源，dx=dy的网格划分下无论是泰勒法还是热平衡法所得的离散方程都是一致的，因此这个问题是完全没有难度的。
首先，划分计算区域：

#确定区域划分
a=100
#方形化区域
dx,dy = a,a #通过更改此项（int）可将区域划分成不同形状，但需要考虑边界条件是否会发生变换

之后确定精度范围：

#确定精确度区间
e = 0.0001

构建二维分布的温度平面，即构建一个dx*dy大小的矩阵：

#构建二维温度平面，此时为0矩阵
t = np.zeros([dx,dy])

随即需要确定边界条件，就像下图边界所述的那样：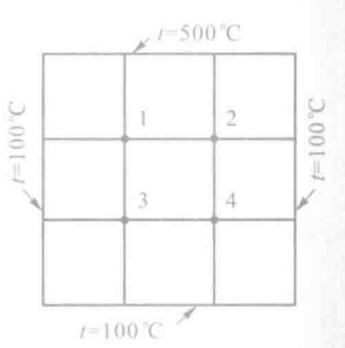

#确定边界条件
t[0]=500
t[1:,0]=100
t[dx-1]=100
t[1:,dy-1]=100

np.zeros方法构建的是0矩阵，应此除了边界外的其余各点都是0，为此需要为这些区域赋值。实际上不赋值也可以啊，但是没有仔细研究初始值与收敛速度的关系。

将待求解内部区域添加初始值

t[1:dy-1,1:dx-1]=100

接下来，为了判断是否一致小于收敛值，我采取的方法是构建一个与t相同大小的矩阵，当这个矩阵全为1时，迭代到目标精度。

#构建与t完全一致待收敛判断序列
#当序列f全为1时，即每一点位置处符合精确度要求
f = np.zeros_like(t)
f[0]=1
f[1:,0]=1
f[dx-1]=1
f[1:,dy-1]=1

之后便通过高斯-赛德尔法进行迭代，这个过程真的十分简单（不考虑优化等情况下）。说实在的，大部分时间都花在查函数用法上了。特别是[:],明明已经做过无数次了。

#通过高斯-赛德尔法进行迭代
x,y=1,1
while (f==1).all() == False:
      for x in range(1,dx-1):
        for y in range(1,dy-1):
            flag=t[x,y]
            t[x,y]=0.25*(t[x-1,y]+t[x+1,y]+t[x,y-1]+t[x,y+1])
            #判断是否符合精确度条件
            if abs(t[x,y]-flag) < e: f[x,y]= 1

在找函数的过程中发现了一个偷懒的好东西：

#偷懒方法做出图像
plt.matshow(t,cmap=plt.cm.Reds)
plt.show()
#输出矩阵，取三位有效值
print(np.around(t,3))

这样既有了可视化方法，还可以给出每一个值出来。
完整代码如下：

import numpy as np
import matplotlib.pyplot as plt
#确定区域划分
a=100
#方形化区域
dx,dy = a,a #通过更改此项（int）可将区域划分成不同形状，但需要考虑边界条件是否会发生变换
#确定精确度区间
e = 0.0001
#构建二维温度平面，此时为0矩阵
t = np.zeros([dx,dy])
#确定边界条件
t[0]=500
t[1:,0]=100
t[dx-1]=100
t[1:,dy-1]=100
#将待求解内部区域添加初始值
t[1:dy-1,1:dx-1]=100
#构建与t完全一致待收敛判断序列
#当序列f全为1时，即每一点位置处符合精确度要求
f = np.zeros_like(t)
f[0]=1
f[1:,0]=1
f[dx-1]=1
f[1:,dy-1]=1
#通过高斯-赛德尔法进行迭代
x,y=1,1
while (f==1).all() == False:
    for x in range(1,dx-1):
        for y in range(1,dy-1):
            flag=t[x,y]
            t[x,y]=0.25*(t[x-1,y]+t[x+1,y]+t[x,y-1]+t[x,y+1])
            #判断是否符合精确度条件
            if abs(t[x,y]-flag) < e: f[x,y]= 1
#偷懒方法做出图像
plt.matshow(t,cmap=plt.cm.Reds)
plt.show()
#输出矩阵，取三位有效值
print(np.around(t,3))

图像如下图所示：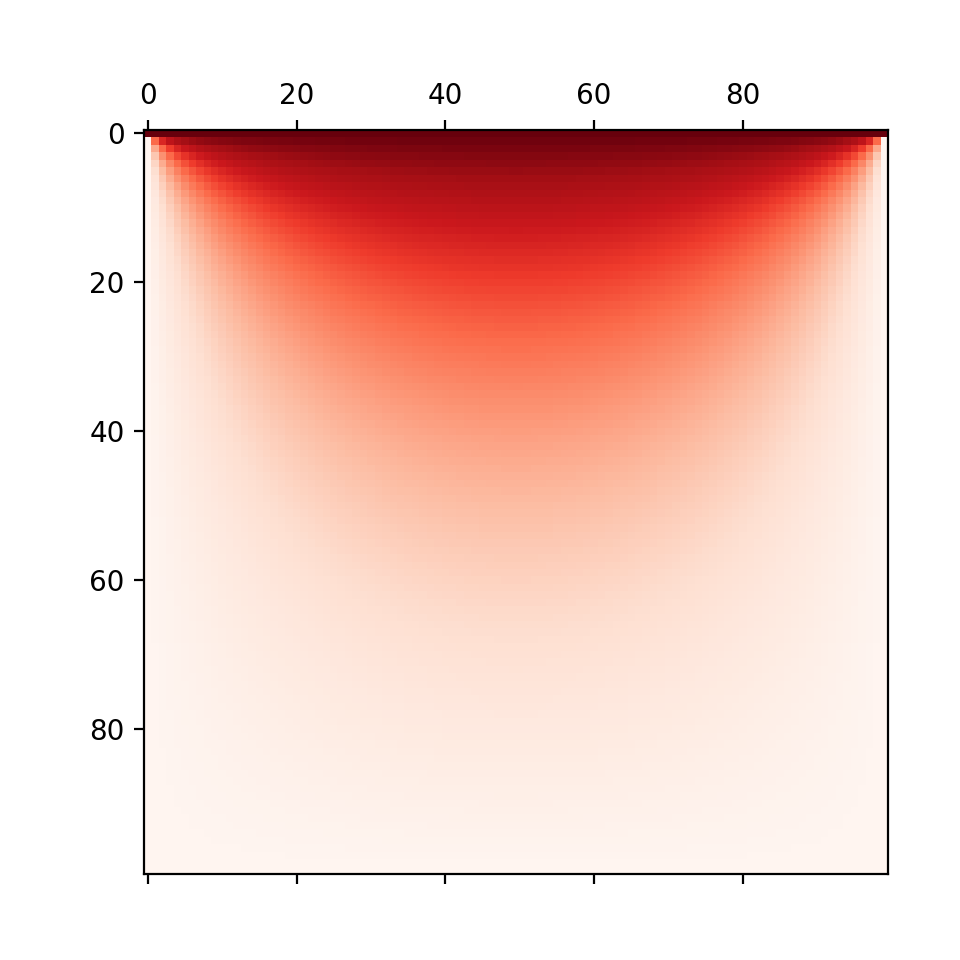

使用Comsol在相同条件下求解，可得如下图像：

还是比较符合的，但是我记得comsol的网格数并不是很多。而且comsol计算在m1不插电的情况下只用了4s，而我的土鳖方法用了90s。不过我竟然可以做出来，就知道前人把这条大路铺的有多平整了。