本次将介绍简单的数值积分(Romberg方法与Gauss—Legender方法)、老生常谈的牛顿迭代法以及经典常用的ODE求解法RK4(四阶龙格-库塔法)。这次重要掌握了Latex方程与MathML的转换,使得能够呈现。并尝试将上篇文章规整化。此外,代码全部上传至https://github.com/DMCXE/Numerical_ComputationRomberg.py GaussLegendre.py NewtonIter.py OED.py Q3.py Q4.py
数值积分
Romberg法
通过复合求积方法的思想,当计算精度不足时,将积分区间 [a,b] 逐级二分,并将二分前后的两个积分值联合考察,可以得到每次二分后的积分递推公式为:
逐次二分可以提高求积公式的精度,可以表示为
其余项可以展开为级数形式,有定理描述为
其中,系数alpha_l与h无关
对其进行外推,将h数次减半,可得到Romberg求积算法:
计算过程为:
- 取k = 0,h=b-a.求
- 依据递推公式求梯形值
- 依据Romberg法求加速值
- 判断精度,否则k+1
衍生的T表为:
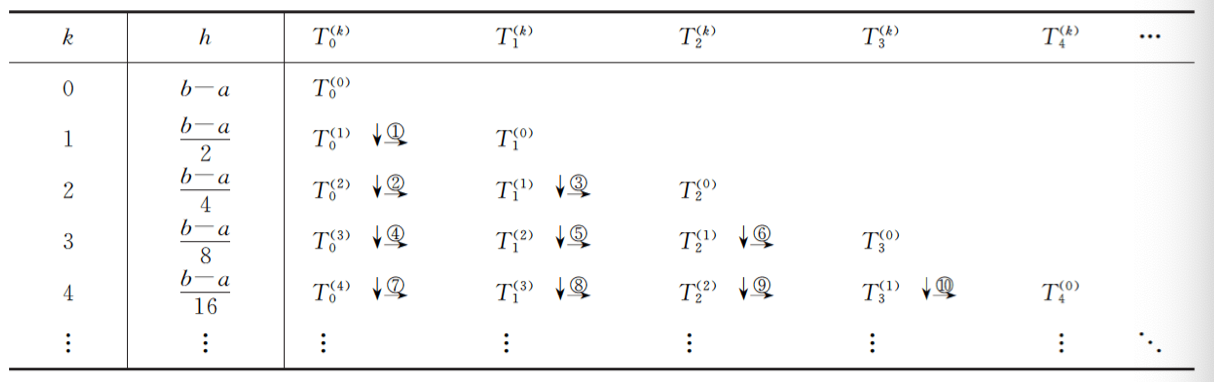
通过以上过程,可以给出编程过程以及求解T表的过程
class Romberg:
def __init__(self, F,min,max,ess):
self.F = F
self.min = min
self.max = max
self.h = max - min
self.ess = ess
def x2k(self,k):
xk = np.array([])
for n in range(0,2 ** (k-1)):
xk = np.append(xk,self.h*(2*n+1)/2**k)
return xk
def T(self,k):
a = self.min
b = self.max
f = self.F
T = np.zeros((k,k))
T[0][0] = 0.5*self.h*(self.F(self.min)+self.F(self.max))
for i in range(1,k):
T[0][i] = 0.5 * T[0][i-1] \
+ (b-a)*(2**(-i))*(np.sum(f(self.x2k(i))))
for i in range(1,k):
for j in range(0,k-i):
T[i][j] = (4**i/(4**i-1))*T[i-1][j+1]\
- (1/(4**i-1))*T[i-1][j]
return T
def caculate(self):
k = 3
delt = 1
while abs(delt)>self.ess:
T = self.T(k)
delt = T[k-1][0]-T[k-2][0]
res = T[k-1][0]
k = k+1
return res,T
def Table(self):
return self.caculate()[1]
def res(self):
return self.caculate()[0]GaussLegendre法
Gauss求积公式的一般原理为
即通过求解2n+2个参数的待定系数方程得到插值求积公式。当[a,b]为[-1,1]时,注意到勒让德多项式在此区间上是正交的。因此可以将勒让德多项式的零点作为高斯求积公式的高斯点。称为Gauss-Legendre求积公式。
下表给出了Gauss-Legendre求积公式的n+1点求积公式系数。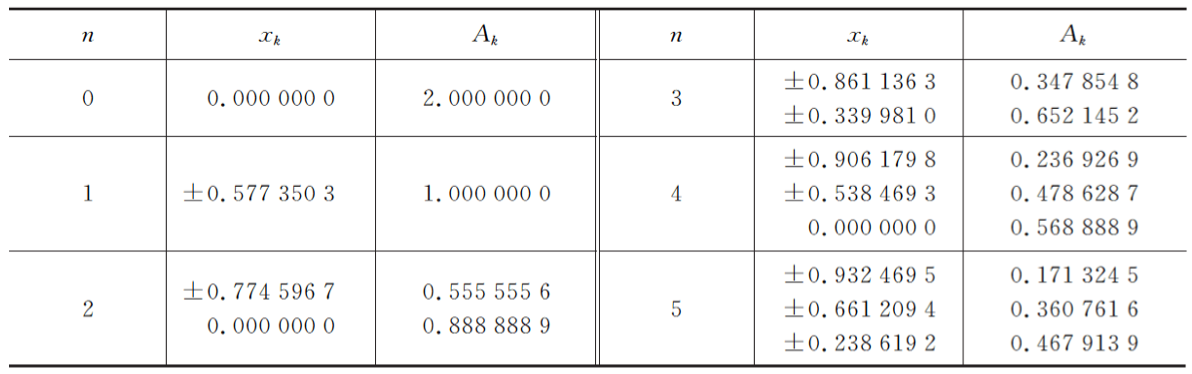
对于三点高斯勒让德求积公式(n=2),为
若被积函数积分区间处于 [a,b] ,则通过变换
改写为
上述算法可以十分容易的翻译为编程语言
"""
三点高斯-勒让德求积公式
"""
class GaussLegendre3:
def __init__(self, F, min, max):
self.F = F
self.min = min
self.max = max
def transaxis(self,t):
return (self.max-self.min)*0.5*t + 0.5*(self.max+self.min)
def res(self):
res = (5/9) * self.F(self.transaxis(-np.sqrt(15)/5)) \
+ (8/9) * self.F(self.transaxis(0)) \
+ (5/9) * self.F(self.transaxis(np.sqrt(15)/5))
res = 0.5*(self.max-self.min)*res
return res牛顿迭代法
牛顿迭代法是一种常见的线性/非线性方程求解法,比如说卡西欧计算器内置的求解功能即运用的是牛顿求解法。对于方程f(x)=0,假设存在近似根x_k,且此点处导数不为0, 利用切线方法在此点处展开,有
即
对于此线性方程,记其根为 x_{k+1}, 计算为
根据上述思路迭代即可。
根据上述思路迭代即可。
class NewtonIter:
def __init__(self, F, f, x0,ess):
self.F = F
self.f = f
self.x0 = x0
self.ess = ess
def Iter(self):
delt = 1
x = self.x0
x0 = x
count = 0
MaxIter = 10000
while delt >= self.ess :
x = x - self.F(x)/self.f(x)
if abs(x)<1:
delt = abs(x0-x)
else:
delt = abs((x0-x)/x)
x0 = x
count += 1
if count >= MaxIter:
x = "超过最大迭代上限10000"
break
return x常微分方程ODE求解
RK4
常用的ODE求解方法为龙格-库塔方法。即增加欧拉法中的节点数提高精度。RK方法可以用公式表示为:
其中
当对r取不同的取值,则对应了不同的方法。四阶RK4方法具备较高的精度,常用于数值计算中。通过数学计算,可以得到RK4的一半表达式为:
将其可简单翻译为编程语言
class RK4:
def __init__(self, F,min,max,totstep,begin):
self.F = F
self.min = min
self.max = max
self.step = (self.max-self.min)/totstep
self.begin = begin
self.totstep = totstep
def slover(self):
f = self.F
x = 0
y = self.begin
yn = np.zeros(1)
yn[0] = y
step = self.step
flag = 1
for i in range(1,self.totstep+1):
K1 = f(x,y)
K2 = f(x+0.5*step,y+0.5*step*K1)
K3 = f(x+0.5*step,y+0.5*step*K2)
K4 = f(x+step,y+step*K3)
y = y + (step/6)*(K1+2*K2+2*K3+K4)
yn = np.append(yn,y)
flag = flag + 1
x = i * step
return yn题目求解
Q3
通过Newton迭代求解
(1)通过Romberg求积计算迭代所需的各项积分值
(2)通过Gauss-le gendre三点公式计算迭代所需的各项积分值
(3)取初值 x_0=0.5 , 选取来自前两问的各节点积分值,用Newton迭代法求根
针对前两问,通过以下方式即可
from Romberg import Romberg
from GaussLegendre import GaussLegendre3
from NewtonIter import NewtonIter
ess = 1e-4
def f(x):
return (1/np.sqrt(2*np.pi))*np.exp(-0.5*(x**2))
"Romberg格式积分值"
def FR(x):
A = Romberg(f,0,x,ess)
return A.res()-0.45
"Gauss-legendre格式积分值"
def FG(x):
A = GaussLegendre3(f,0,x)
return A.res()-0.45
"第一问:Romberg积分值"
visualize(FR,0,10,50)
print(Romberg(f,0,5,ess).Table())
"第二问:Gauss-legendre格式积分值"
visualize(FG,0,10,50)对于Romberg积分值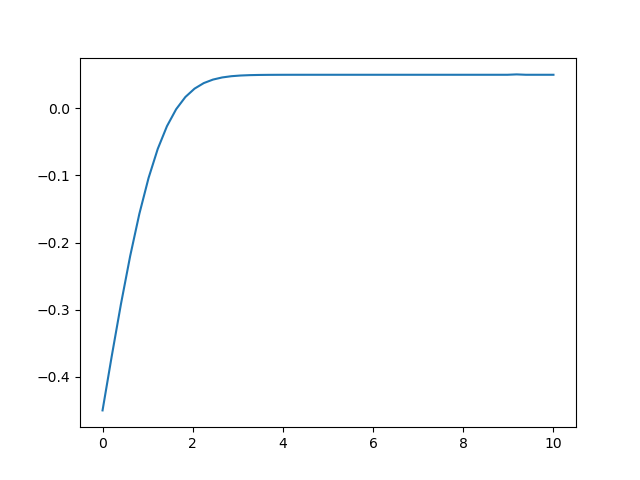
在x=5时形成的T表为(经过了转置)
[[0.99735942 0.54250046 0.50000233 0.4999995 0.49999965 0.4999997 ]
[0.39088081 0.48583629 0.49999856 0.49999971 0.49999971 0. ]
[0.49216665 0.50094271 0.49999978 0.49999971 0. 0. ]
[0.50108201 0.49998482 0.49999971 0. 0. 0. ]
[0.49998051 0.49999977 0. 0. 0. 0. ]
[0.49999979 0. 0. 0. 0. 0. ]]
对于三点Gauss-lengendre的积分值
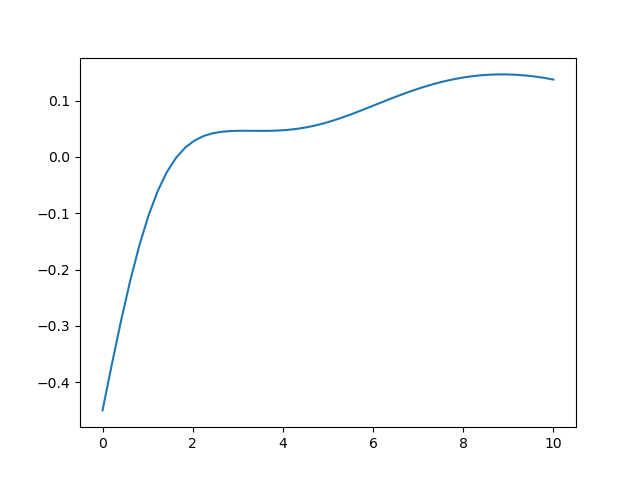
不难发现当x较大时其精度相较于Romberg较差。这是由于插值精度决定的。
对于第三问:
通过对以上两个积分方法带入到牛顿迭代中,
Romberg方法:1.6448571505297174
Gauss-lengendre方法:1.6451738240002383
Q4
在题目条件下求解方程:
其中:
计算在0.2s后形成多少单位的KOH
计算代码为:
'''KOH生成速率的ODE'''
def F(x,y):
k = 6.22*1e-19
n1 = 2*1e3
n2 = 2*1e3
n3 = 3*1e3
return k*((n1 - 0.5*y)**2)*((n2 - 0.5*y)**2)*((n3 - 0.75*y)**3)
"初值和边界条件"
time_start = 0
time_end = 0.2
totstep = 100
boundary0 = 0
"实例化"
A = RK4(F,time_start,time_end,totstep,boundary0)
koh = A.slover()
"0.2s时产率为"
print(koh[-1])
"趋势可视化"
plt.figure()
xx = np.linspace(time_start,time_end,totstep+1)
plt.plot(xx, koh)
plt.show()
反应趋势与数据为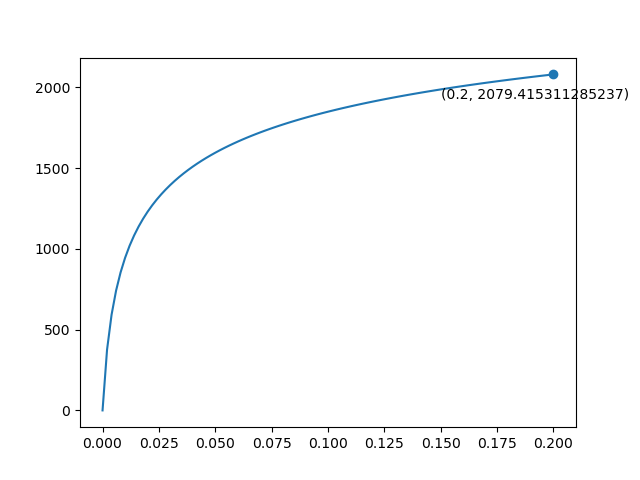

骞神!你是我的神!!!

