本次介绍直接通过求解线性方程得到二维平板的稳态传热。当然,醉翁之意不在酒,拉普拉斯方程代表的一众物理问题都可以迎刃而解。本内容上传至学院共享仓库https://github.com/euaurora/HappyShares-CNST-HEU/tree/main/传热学/平板传热的矩阵法%20-by%20DMCXE以及个人博客。推荐观看pdf版本。
1 回顾
严格来说是前年,介绍了如何通过Gauss–Seidel迭代方法求解二维平板传热方程。以Gauss–Seidel、Jacobi等为代表的一种方法均通过迭代进行矩阵的求解。由于其收敛曲线平滑,因而对于满足此类方法的矩阵,复杂与否都可以得到期望的结果。但是缺点显而易见,在上一篇文章中,100X100的网格计算了90s,这显然是不可接受的。对于传热方程、或者对于形式上类似的方程, 我们有更好的方法进行求解。
2 矩阵运算快速求解
2.1 二维传热方程的矩阵运算
无内热源,稳态的二维传热方程为:
空间差分可以得到:
考虑均匀的网格划分$\Delta x= \Delta y$, 上述方程可以化简为:
根据《传热学》,这一步就可以进行迭代表达式的拆分了。直观来看,似乎并没有什么好方法去求解这个复杂的线性方程组。
2.1.1 在一维情况下思考
如果我们退一步,考虑一维的传热方程
我们遍历每一种可能情况:
注意到可以写为一个系数矩阵A_{NxN}与T_{Nx1}的乘积,且系数矩阵只有三个对角!(不考虑周期边界条件)
也就是说,传热方程可以写成一个线性方程组AT=Z。求解矩阵的线性方程组,自然而然的就想到几个方法:
- 求逆。T=A^{-1}Z。
- 分解。A=LU,LUT=Z,b=UT,Lb=Z
也就是说,这个方程好不好解,除了与本身的规模大小有关外,还与系数矩阵A的性质有关。我们重新观察A,发现他是:
- 稀疏的。只有几个对角。——> 稀疏矩阵的逆往往是稠密的,稠密矩阵进行运算复杂度是N^3
- 对称的。A=A^{T}
- 在有边界值的情况下,是非奇异的。
A的性质非常好,也就是说可以通过特殊的矩阵分解方法进行快速矩阵运算求解。举个例子,加入对于一维杆,两端温度已知,上述矩阵为:
A构成了三对角矩阵,求解三对角矩阵的线性方程组可以使用追赶法:
对于方程组
利用
1.计算{beta_i}的递推公式:
2.求解Ly=f
3.求解Ux = y
即可实现快速计算,即一种特殊LU分解。
2.1.2 在二维中
回到
如果假设我们存在一个系数矩阵A_{NxN}$与描述平面温度分布的矩阵T_{NxN},这样的稠密矩阵相乘是非常繁琐的。自然的,类比一维空间差分的处理,自然的想到该方程对于了某个系数矩阵A_{NxN}与温度矩阵T_{NxN}的乘积,写为AT=P_{NxN}。但是我们并没有很方便的工具去求解此问题(虽然可以考虑令T=A^{-1}P)。保持一维情况下求解稀疏矩阵的策略不变,可以将空间差分网格依据纵向拼接,构成T_{N^2x1}、P_{N^2x1}以及系数矩阵A_{N^2xN^2}, 即
系数矩阵A可以通过观察差分方程的格式得到:(暂时不考虑Delta x)
即系数矩阵A为分块矩阵,简化表示为:
其中分块矩阵T,E,Z分别为
显然的,二维问题又简化为求解线性方程组的问题,且对应的系数矩阵仍然是稀疏的。即对于N^2 x N^2规的矩阵,仅有九条对角线非0,5N^2个非0元素。
2.2 懒人求解工具
有很多种求解稀疏矩阵的工具,当然可以手搓,但是造轮子需要有一个非常扎实的数学基本功,至少我是不具备的。为此,介绍一种好用的稀疏矩阵线性方程组求解工具。
import scipy.sparse as sp
from scipy.sparse.linalg import spsolve2.2.1 构建稀疏矩阵的方法
采用沿对角线构建稀疏矩阵,通过
diags = np.array([k1,k2,k3,...])
vals = np.vstack((e1,e2,e3,...))
mtx = sp.spdiags(vals,diags,N,N)方式生成。其中,diags指定了对角线元素e所处的位置。k=0处于主对角线,k<0处于主对角线下方,k>0处于主对角线上方。对角线元素e是长度为N的向量,写入矩阵时,K<0时舍弃尾部元素,K>0时舍弃头部元素;vals将所有对角线向量组成多维向量;sp.spdiags()即根据上述规则生成规模为NXN的矩阵。
2.2.2 求解稀疏线性方程组
scipy.sparse.linalg提供了多种处理稀疏矩阵的工具。但是需要将矩阵的储存格式转换为按行/按列排列的形式。比如
mtx = sp.lil_matrix(mtx)
mtx = sp.csr_matrix(mtx)之后,通过
T = spsolve(mtx, b)即可快速的实现求解。
3 稳态传热数值解
无内热源,稳态的二维传热方程为
在一个长为0.6m,宽为0.4m的矩形板,左右下三侧温度均为100度,上侧温度500度。横纵均分为128个网格,条件表示为
Lx = 0.6
Ly = 0.4
Nx = 128
Ny = 128
dx = Lx/Nx
dy = Ly/Ny
"配置边界温度"
T_right = 100
T_left = 100
T_up = 500
T_down = 100接下来,生成稀疏矩阵(考虑边界条件条件)
def Lmatrix_withBound(Nx,Ny,bound,dx,dy):
'''
Nx: Nx=Ny,差分网格横/纵方向上的节点数
bound: nx2数组,给出了不同边界位置的坐标
'''
#对边界索引进行变换
bou = (np.array([num[0]+Nx*num[1] for num in bound]))
N_grid = Nx*Ny
e00 = np.ones(N_grid)
e00 /= dy**2
e00[bou] = 0
e00 = np.roll(e00, -(Nx ** 2 - Nx))
e000 = np.ones(N_grid)
e000 /= dy**2
e000[bou] = 0
e000 = np.roll(e000, (Nx ** 2 - Nx))
e0 = np.ones(N_grid)
e0 /= dy**2
e0[bou] = 0
e0 = np.roll(e0, -Nx)
e6 = np.ones(N_grid)
e6 /= dy ** 2
e6[bou] = 0
e6 = np.roll(e6, Nx)
e1 = np.zeros(N_grid)
e1[np.array(range(Nx-1,N_grid,Nx))] = 1
e1 /= dx ** 2
e1[bou] = 0
e1 = np.roll(e1,-Nx+1)
e5 = np.zeros(N_grid)
e5[np.array(range(Nx - 1, N_grid, Nx))] = 1
e5 /= dx ** 2
e5[bou] = 0
e5 = np.roll(e5, Nx )
e2 = np.ones(N_grid)
e2[np.array(range(Nx, N_grid, Nx))]=0
e2 /= dx ** 2
e2[bou] = 0
e2 = np.roll(e2,-1)
e4 = np.ones(N_grid)
e4[np.array(range(Nx-1, N_grid, Nx))] = 0
e4 /= dx ** 2
e4[bou] = 0
e4 = np.roll(e4, 1)
e3 = (-2*np.ones(N_grid)/dx**2)+(-2*np.ones(N_grid)/dy**2)
e3[bou] = 1
diags = np.array([-(Nx ** 2 - Nx),-Nx,-Nx+1, -1 , 0 , 1 , Nx-1,Nx,(Nx ** 2 - Nx)])
vals = np.vstack((e00 ,e0, e1, e2 , e3 ,e4, e5, e6,e000))
mtx = sp.spdiags(vals,diags,N_grid,N_grid)
mtx = sp.lil_matrix(mtx)
mtx = sp.csr_matrix(mtx)
return mtx之后,依据边界温度条件构造稀疏矩阵与右端向量:
def bound_condition(T_left,T_right,T_up,T_down,Nx,Ny,dx,dy):
T_right = T_right
T_left = T_left
T_up = T_up
T_down = T_down
RHS = np.zeros(Nx * Ny)
"配置边界网格"
bound_right = (Ny - 1) * np.ones((Nx, 2))
bound_right[:][:, 0] = np.arange(0, Nx)
bound_liner_right = np.array([num[0] + Nx * num[1] for num in bound_right]).astype(int)
bound_left = np.zeros((Nx, 2))
bound_left[:][:, 0] = np.arange(0, Nx)
bound_liner_left = np.array([num[0] + Nx * num[1] for num in bound_left]).astype(int)
bound_up = np.zeros((Ny, 2))
bound_up[:][:, 1] = np.arange(0, Ny)
bound_liner_up = np.array([num[0] + Nx * num[1] for num in bound_up]).astype(int)
bound_down = (Nx - 1) * np.ones((Ny, 2))
bound_down[:][:, 1] = np.arange(0, Ny)
bound_liner_down = np.array([num[0] + Nx * num[1] for num in bound_down]).astype(int)
bound = np.vstack((bound_left, bound_right, bound_up, bound_down)).astype(int)
#添加边界上的解
RHS[bound_liner_left] = T_left
RHS[bound_liner_right] = T_right
RHS[bound_liner_up] = T_up
RHS[bound_liner_down] = T_down
#生成稀疏矩阵
Lmatx = Lmatrix_withBound(Nx,Ny, bound, dx,dy)
return Lmatx,RHS
通过稀疏矩阵线性方程求解器得到温度的解,但是此温度是一个向量,需要重新转换为矩阵的形式。
T_grid = spsolve(Lmatx,RHS)
#转化为矩阵形式
T_martix = T_grid.reshape(Nx, Nx).T
#可以通过查看矩阵的值近似代替解的图像
plt.matshow(T_martix)在计算0.12967610359191895s后,得到解的图像: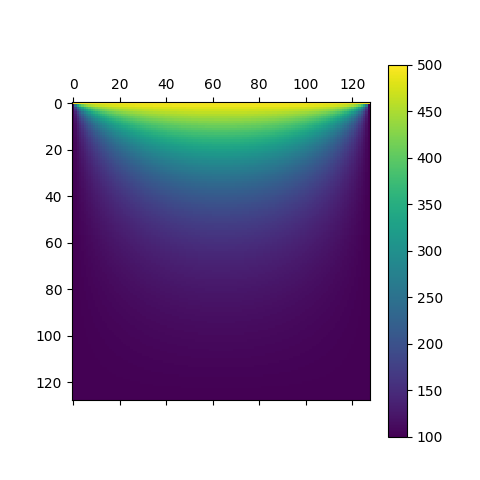
当网格为256x256时,在计算0.9013581275939941s后,得到解。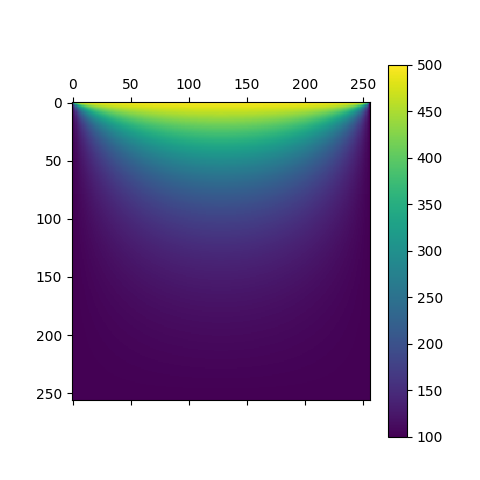
相比于迭代法,得到了将近700倍的加速,且误差仅存在于数据的储存上。
完整代码为:
def main():
Lx = 0.6
Ly = 0.4
Nx = 256
Ny = 256
dx = Lx/Nx
dy = Ly/Ny
"配置边界温度"
T_right = 100
T_left = 100
T_up = 500
T_down = 100
"配置系数矩阵A与向量b"
Get_bound = bound_condition(T_left,T_right,T_up,T_down,Nx,Ny,dx,dy)
Lmatx = Get_bound[0]
RHS = Get_bound[1]
T_grid = spsolve(Lmatx,RHS)
T_martix = T_grid.reshape(Nx, Nx).T # 将矩阵
return T_martix
if __name__ == "__main__":
Lx = 0.6
Ly = 0.4
Nx = 256
Ny = 256
st = time.time()
T_martix = main()
end = time.time() - st
print(end)
fig = plt.figure(figsize=(5, 4), dpi=80)
plt.cla()
Tp = plt.matshow(T_martix)
plt.colorbar(Tp)
plt.show()
评论 (0)