本次将通过改进RK4（四阶龙格-库塔法）法构建ODE求解器以获得对于微分方程组的求解，并通过相关大作业的实力内容进行计算验证。通过此方程组的建立，对于Modelica运行时的一些event耗时问题也产生了一些思考与理解。此外，代码全部上传至https://github.com/DMCXE/Numerical_Computation

ODE.py Homework.mo

RK4方法的回顾

常用的ODE求解方法为龙格-库塔方法。即增加欧拉法中的节点数提高精度。RK方法可以用公式表示为：

其中

当对r取不同的取值，则对应了不同的方法。四阶RK4方法具备较高的精度，常用于数值计算中。通过数学计算，可以得到RK4的一般表达式为：

但通常微分方程是通过微分方程组的形式出现，比如说传染病模型SEIR。而在《数值计算二》中构建的ODE求解器只能够求解单独的微分方程，局限性较高。开发通用的微分方程组求解器是必须需要解决的。

RK4方法对方程组的适应改进

在这里，RK4是一种前向方法。因此当函数化为方程组时，只需要将方程指定为向量格式、并在自变量统一时，将因变量写成向量格式。若f(x,y)表示的形式是f(t,x)，即写为f(t,x1,x2,x3,x4)。RK4的数学形式是支持向量化的，因为按照上述方法处理后，各个变量的相互关系能够通过向量组缩影体现出来。

在求解器中，求解过程完全一致，但与求解单方程不同的是，我们需要指定方程组在的方程个数N，并通过该数构建用于储存结果的Nx1矩阵。我们把主要的处理放在了对于函数组表达的预处理上。

import numpy as np
class RK4_for_equations:
    def __init__(self, F,n,min,max,totstep,begin):
        self.F = F
        self.n = n #指定方程组的个数
        self.min = min
        self.max = max
        self.step = (self.max-self.min)/totstep
        self.begin = begin
        self.totstep = totstep

    def slover(self):
        f = self.F
        x = 0
        y = self.begin
        yn = np.zeros((self.n,1))
        yn[:,0] = y
        step = self.step
        flag = 1
        for i in range(1,self.totstep):
            K1 = f(x,y)
            #print("K1:",K1)
            K2 = f(x+0.5*step,y+0.5*step*K1)
            #print("K2:",K2)
            K3 = f(x+0.5*step,y+0.5*step*K2)
            #print("K3:",K3)
            K4 = f(x+step,y+step*K3)
            #print("K4:",K4)
            y = y + (step/6)*(K1+2*K2+2*K3+K4)
            yn = np.append(yn,y.reshape(self.n,1),axis=1)
            flag = flag + 1
            x = i * step
        return yn

对于传入函数的预处理

简单的来说，我们需要把传入函数写为F(x,y)=[f1(x,y,...,fn(x,y)]格式。以下通过一个实际案例进行描述：
已知蒸汽发生器水位控制系统的微分方程如下：

求解方程组的数值解。该方程的参数部分由一个参数表给出，在程序里，将参数写成类的方式调用。对于该方程组，首先需要定义由参数生成的函数类：

class Functions():
    def __init__(self,G1,G2,G3,tau_0,tau,beta,xi,qe,qv):
        self.G1 = G1
        self.G2 = G2
        self.G3 = G3
        self.tau_0 = tau_0
        self.tau = tau
        self.beta = beta
        self.xi = xi
        self.qe = qe
        self.qv = qv
    def f1(self,t,x):
        return self.G1*(self.qe(t) - self.qv(t))
    def f2(self,t,x):
        x2 = x[1]
        return -x2/self.tau_0 + self.G2 * self.qv(t)/self.tau_0
    def f3(self,t,x):
        x4 = x[3]
        return x4/self.tau**2 - self.G3*self.beta*self.qe(t)/self.tau
    def f4(self,t,x):
        x3 = x[2]
        x4 = x[3]
        return -x3-2*self.xi*x4/self.tau+(2*self.xi*self.beta-1)*self.G3*self.qe(t)

这里Function类中的函数传入参数分别为单标量时间t以及因变量的集合x=[x1,x2,x3,x4]。第一个方程f1是与x关的常数方程，第二个方程f2是仅与自生相关的微分方程，第三与第四个方程见形成了耦合的微分方程组。通过向量化变量，实现了多变量间的耦合。
在该题目中，参数qe与qv是与时间相关的可变参数，定义为：

qv = lambda t: 0
qe = lambda t: 1 if t>=5 else 0

需要注意的是，所有和时间相关的变量参数需要在构建方程组时依据函数的格式单独声明，因为我们的ODE求解器仅接受函数对象并求解（所有的可变参数相当于传入了指向参数变化模式函数的地址）。

当我们实例化class Function()后，即可通过构建函数或者lambda表达式的格式构建方程组表达式：

F = lambda t,x: np.array([Func.f1(t,x),Func.f2(t,x),Func.f3(t,x),Func.f4(t,x)])

构建的方程组表达式仅需要传入自变量t与函数x，这与求解器的格式一致。求解过程为：

solver1 = ODE.RK4_for_equations(F,4,0,50,step,x0).slover()
#F:方程组
#4:方程组规模
#0:start time
#50: end time
#step:1000,总步长
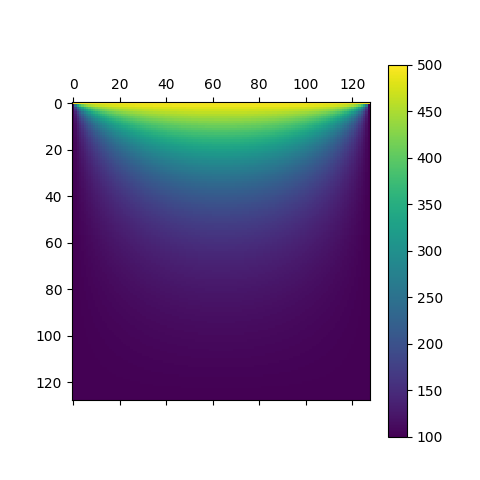
#x0: 初值

最后我们得到的结果为：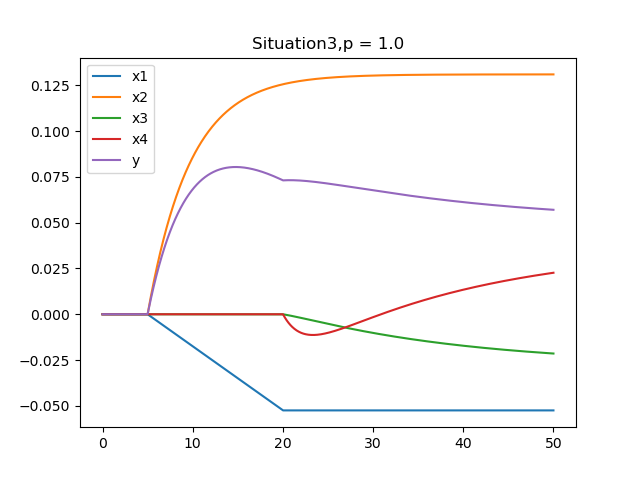

获得关于Modelica的启示

Modelica是一个面向物理方程的语言，在编写程序的时候时时会被气晕，比如说：难以设置时变参数、难以重新为变量赋值、频繁的事件（event）处理耗费巨量的时间、长数组耗时等问题。在写完ODE的方程组求解器后，让我对Modelica有了全新的思考。Modelica的编译流程为：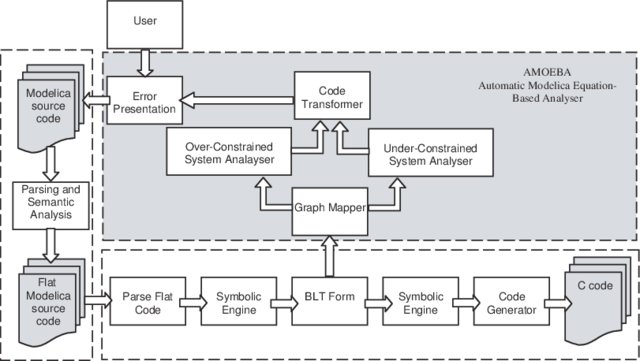


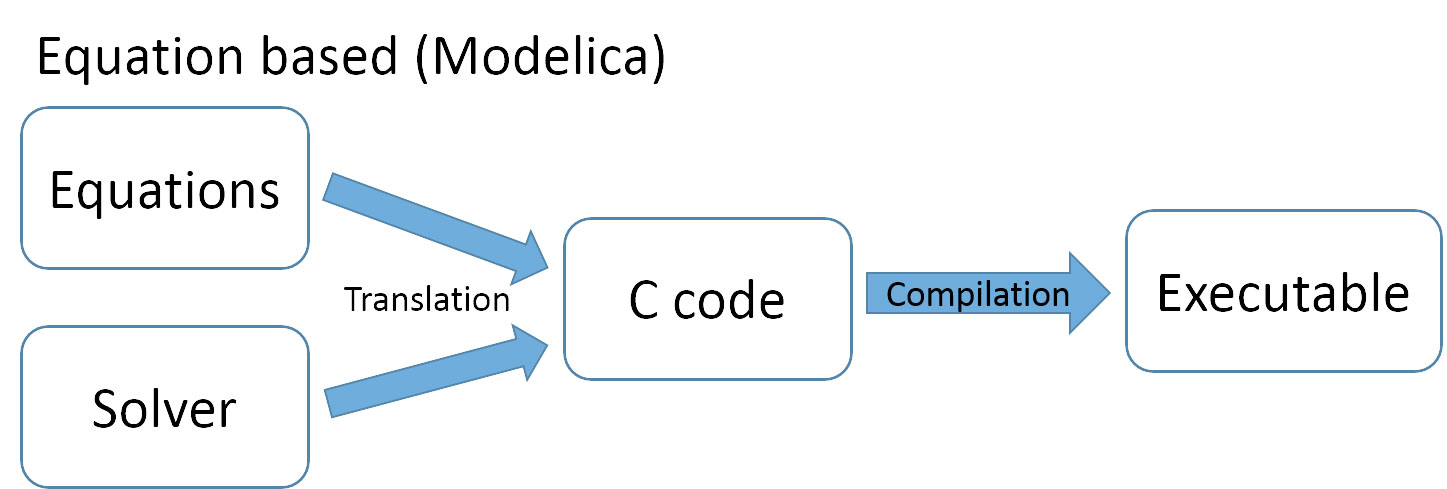
Equations与Solver是分开的两部分，在用户编写组件代码并配置求解器后，Modelica会将用户方程转译为求解器支持的格式，并转译为C代码，最后编译。这个过程等价于我们之前先预处理方程组，再调用求解器求解的过程。

这也解释为，为什么在可（时）变参数在modelica中如此复杂，需要通过reinit、algrothm或者function的方式实现：正如上一节所说的，求解器只负责随时间求解，可变参数需要传入一个指向函数的地址。站在个角度，reinit是三个方法中最慢的，因为涉及了event的判断。

当我们改变条件，某些参数不再是时变了，而是根据解改变，比如说：粒子运动的周期边界条件（如果粒子撞到壁了，就取余）。这时我们就需要先试着求解一段时间，判断解是否触发条件，再接着尝试一段时间，并且将方程的预处理重新执行一遍。

Modelica从这个角度上类似于面向对象编程而不是面向过程编程，比如说当我们在C中处理碰撞问题，我们只需要随着每一个时步去观察便可以判断碰撞结果。但在Modelica中，由于求解器与方程的分离，求解器不得不找到一些分化的方法，以某种规律输出结果去猜测是否触发碰撞。当方程的规模变大后，这样的处理耗时将不断的累积起来，直到我们无法接受的程度。换句话说：纯粹依赖Modelica的事件处理是面向对象的、但我们可以将面向过程表达式写在方程组的构建中。

这也告诉我们，如果一定要处理复杂的、参数随着状态频繁改变的系统，最好将这些变化条件全部打包成Function的形式、在其中用面向过程的方法处理。保证我们的求解器仅需要承担求解的任务。

举个例子，还是上面的稳压器求解，在Modelica中，使用rungeketta法

• 使用Function的方式：

  • qv与qe的代码描述为：

    function qvt
      input Real t;
      output Real qv;
      algorithm
        if t < 5 then
        qv := 0;
      else
        qv:= 1;
      end if;
    end qvt;
    
    function qet
      input Real t;
      output Real qe;
      algorithm
        if t < 20 then
        qe := 0;
      else
        qe:= 1;
      end if;
    end qet;
    
    equation
    qv = qvt(time);
    qe = qet(time);

  • 计算资源开销：

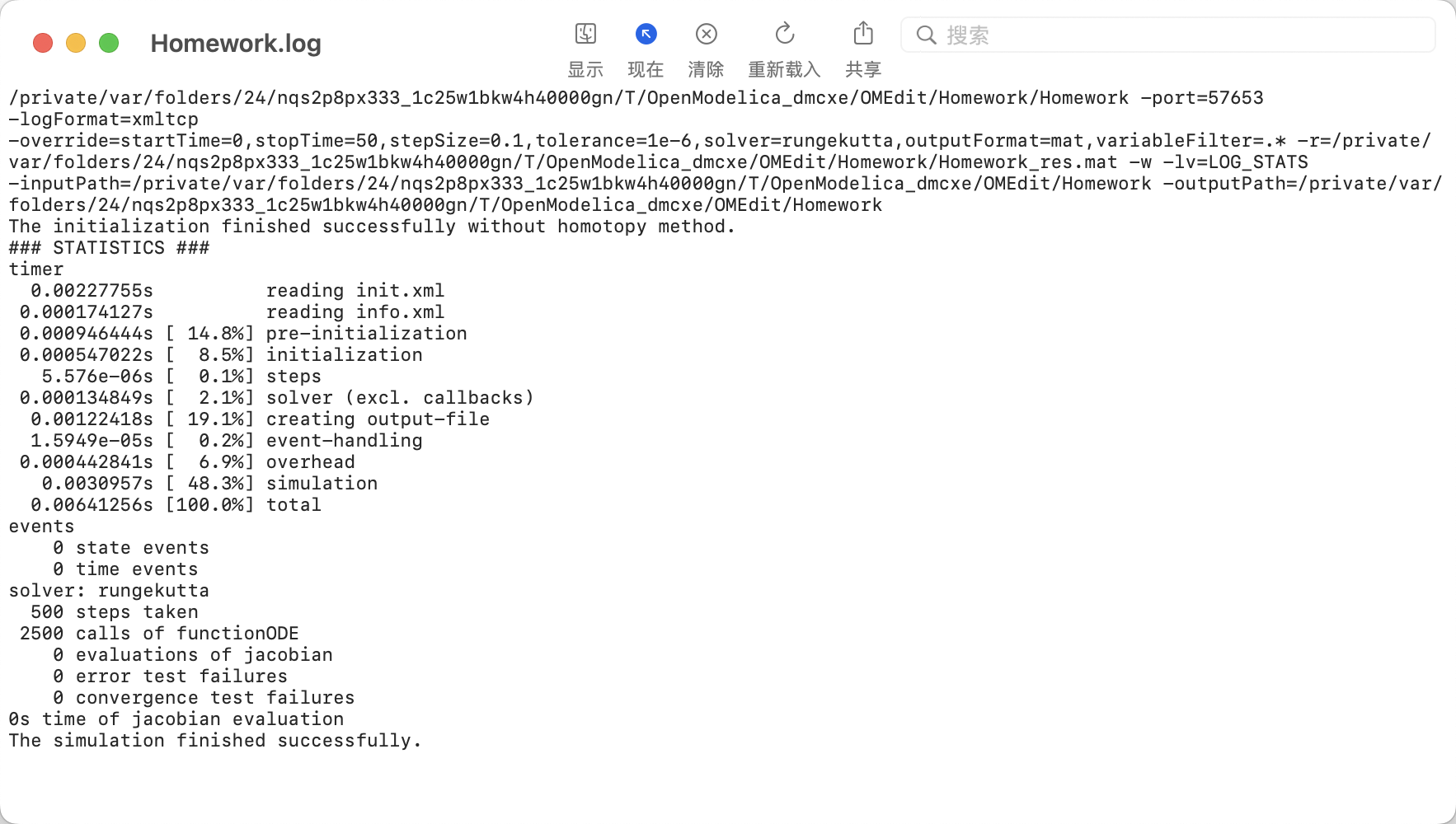
• 使用reinit的方式：

  • qv与qe代码描述为

    equation
    when time >= 20 then
      reinit(qe,1);
    end when;
    when time >= 5 then
      reinit(qv,1);
    end when;
    der(qv) = 0; //保持常数特性
    der(qe) = 0; //保持常数特性

  • 计算资源开销

不难发现，在整体上，函数化方法比事件处理方法快不到0.001s，但是在事件处理上消耗了更少的时间，函数化方法主要时间消耗在模拟上，而事件化方法主要消耗在方程的初始化上。在500个步长下，函数化方法总共耗费500个时步，而事件化方法耗费755个时步，产出了时步的冗余。在1000时步下，函数方法仍是1000步，事件化方法耗时则达到了1505步。受限于方程规模，该比较肯定存在不足之处。但是总体上应当符合这个思路。

（不考虑dassl求解器，dassl求解器的步长是自适应的，与我们指定的无关，它有着非常不一样的处理模式和结果，很有意思）