主要想体现的是把绘制matlab的程序改成了python，其实就换个命令得了
第三章没写是因为全是推导题，我只会xjb推，这一章其实大部分也是xjb推

等离子体诊断方法-第四章：等离子体辐射

题目一

在讨论高温等离子体中的各种具体的辐射过程之前，需要讨论一下等离子体中辐射的输运问题。考虑等离子体本身是个辐射源，又是吸收介质，试讨论表面辐射量 B （（或面辐射度 W ）与体辐射密度 U （或辐射率  ）之间的联系。

面辐射度$W$定义为单位面积的光源表面向外辐射的总功率。

表面辐射量$B$定义为电位光源表面积沿其法线方向在单位立体角内的辐射功率。

体辐射度$U$定义为单位体积辐射源所辐射的总功率。

体辐射率$\eta$ 定义为对于射向各个方向的辐射，沿着某一方向的单位立体角来计算体辐射度，即为辐射率。

对于表面辐射度与表面辐射量，根据定义具有下述关系

B = \frac{d W}{\cos θ d Ω}

其中θ为辐射方向与表面法线之间的夹角。若各个方向的表面亮度相同，则该辐射体被成为余弦辐射体或理想辐射体，能够建立如下积分关系：

W = B \int_{2 π} \cos θ d Ω = π B

辐射通量Φ定义为每单位时间内通过某一面积的辐射能量

辐射强度I定义为沿某一方向的单位立体角内、单位时间内通过单位视在面积的辐射能量

辐射通量与辐射强度具有下述关系：

I_{f} = \frac{d^{2} Φ_{f}}{d Ω d S \cos θ}

即在光源表面处的辐射强度就是光源的表面亮度B

仅考虑辐射在无损耗、各向同但略不均匀的介质内输运过程，建立一个直圆柱体积元，其端面积为dS，厚度为dx。从前断面射入的辐射强度为If、立体角为dΩ1，射入方向与端面法线夹角为θ1。从后端面射出辐射的数值分别为If+dIf、dΩ2、dθ2。根据稳态条件下辐射能量守恒原则，有

\nabla \cdot Φ = 0

在x方向上有

(I_{f} + d I_{f}) \cos θ_{2} d Ω_{2} d S - I_{f} \cos θ_{1} d Ω_{1} d S = 0

由斯涅尔定律nsinθ=const，对于入射出射光线：

\frac{d Ω_{2}}{d Ω_{1}} = \frac{\sin θ_{2} d θ_{2}}{\sin θ_{1} d θ_{1}} = \frac{\sin θ_{2}}{\sin θ_{1}} \cdot \frac{n \cos θ_{1}}{(n + d n) \cos θ_{2}} = (\frac{n}{n + d n})^{2} \frac{\cos θ_{1}}{\cos θ_{2}}

化简为

\cos θ_{2} d Ω_{2} = (\frac{n}{n + d n})^{2} \cos θ_{1} d Ω_{1} \approx (1 - 2 \frac{d n}{n}) \cos θ_{1} d Ω_{1}

将上市带入x方向上的表达式，可以获得

\frac{d I_{f}}{I_{f}} = 2 \frac{d n}{n}

即

\frac{I_{f}}{n^{2}} = c o n s t

上式构成了辐射在无损耗、各向同但略不均匀的介质内的输运过程。
对于等离子体，由于等离子体本身既是辐射源，又是吸收介质，因此辐射在等离子中传播时既会随着折射率率的变化而引发强度变化，又会由于自身产生一定量的辐射增量。折射率变化引发的的辐射强度变化可以表示为：

(d I_{f})_{1} = 2 \frac{I_{f}}{n} \frac{d n}{d x} d x

等离子体本身的谱辐射率与谱吸收系数分别用n_f与n_α表示。若等离子体足够大，沿着某一方向观察有, 有等离子体辐射产生的增量为

(d I_{f})_{2} = n_{f} d x

由于等离子体吸收产生的衰减为

(d I_{f})_{3} = - α_{f} I_{f} d x

等离子体内总辐射能量守恒，可以得出：

\frac{d I_{f}}{d x} = 2 \frac{I_{f}}{n} \frac{d n}{d x} + n_{f} - α_{f} I_{f}

整理，等离子体的辐射输运方程表述为：

n^{2} \frac{d}{d x} (\frac{I_{f}}{n^{2}}) = n_{f} - α_{f} I_{f}

利用dτ=-α_fdx，将等离子体辐射输运方程改写为：

\frac{d}{d τ} (\frac{I_{f}}{n^{2}}) = \frac{I_{f}}{n^{2}} - \frac{η_{f}}{n^{2} α_{f}}

对辐射输运方程沿观察方向进行路径积分，即可获得表面辐射量B。假设离子温度T是均匀的，且不考虑n变化：

I_{D, f} = I_{0, f} \exp (- τ_{D, f}) + B_{f} (T) [1 - \exp (- τ_{D, f})]

其中，I_{0,f}表示外辐射源在等离子体内沿观察方向的初始辐射强度；D为观察方向等离子体的厚度；B_f=η_f/n^2α_f为黑体辐射；τ_{D,f}=∫_0^Dα_fdl为光学厚度，当τ_{D,f}>>1时，表面辐射量趋近于黑体辐射亮度

当等离子体均匀时，α_f为常数，则

τ_{D, f} = \int_{0}^{D} α_{f} d l = α_{f} D

当τ_{D,f}<<1时，被成为光学薄，在无外部辐射源下：

I_{D, f} = B_{f} (T) [1 - \exp (- τ_{D, f})] \approx B_{f} (T) α_{f} D

即

B = I_{D, f} = B_{f} α_{f} D = \frac{n_{f}}{n^{2}} D = \frac{U_{f}}{4 π} D

题目二

电子回旋辐射应用于等离子体诊断最成功的是托卡马克诊断。在托卡马克等离子体情况下，辐射频率与大半径位置有关，因而可通过改变改变本振源的频率来获得私同空间位置的电子温度。假设有托卡马克磁轴（（径向和极向位置为零）磁场大小 0 B T = 2.2486 ，大半径 0 R m =1.85 （。本振源的中心频率设定为 ’ECE_FLO=105.1:2:167.1’（从 105.1GHz 以 2GHz 的间隔增长到 167.1GHz），考虑本振频率对应二解电子回旋频率。根据’mcrossection123.m’（（托卡马克截面的绘制代码），在其上完成 ECE 诊断在中平面（极向位置为零）上沿径向的观测点的空间位置的计算并绘制出来。请将添加的代码贴在作业中

在等离子体中，电子沿磁力线做回旋运动，其电子回旋频率，即Larmor频率及其谐波频率为：

ω = n \frac{e B}{γ m_{e}}

其中，n为谐波数，e为电子电荷数，B为磁场强度，m_e为电子质量，γ为相对论因子，这里考虑非相对情况，约为1。在Tokamak中，磁场随着大半径R变化为:

B = \frac{R_{0} B_{0}}{R}

其中，R_0为磁轴处对应的半径大小，B_0为磁轴处磁场的强度。结合上述两式，可以得到电子回旋频率及其谐波与所处大半径位置之间的关系为：

ω = n \frac{e R_{0} B_{0}}{m_{e} R}

根据直接线性求解或者逆向求解，可以得到在给定频率下观测空间位置的分布：

[2.21576223, 2.17438479, 2.13452439, 2.09609911, 2.05903281, 2.02325465, 1.98869864, 1.9553032 , 1.92301082, 1.89176776, 1.86152367, 1.8322314, 1.80384671, 1.77632808, 1.74963644, 1.72373509, 1.69858943, 1.67416686, 1.65043665, 1.62736975, 1.60493874, 1.58311768, 1.56188203, 1.54120854, 1.52107518, 1.50146106, 1.48234634, 1.4637122 , 1.44554072, 1.4278149, 1.41051854, 1.39363621]

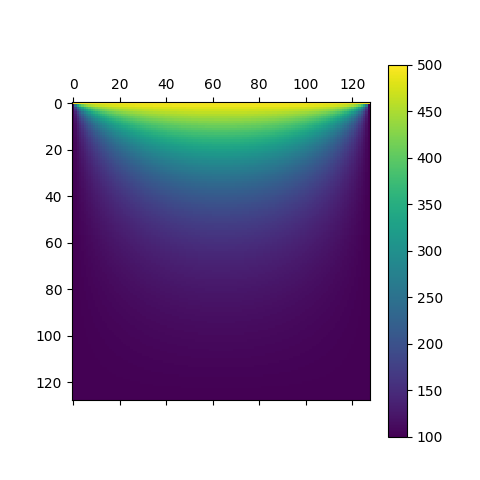
在图上的位置为：基于matlab的绘图代码可以改写为python形式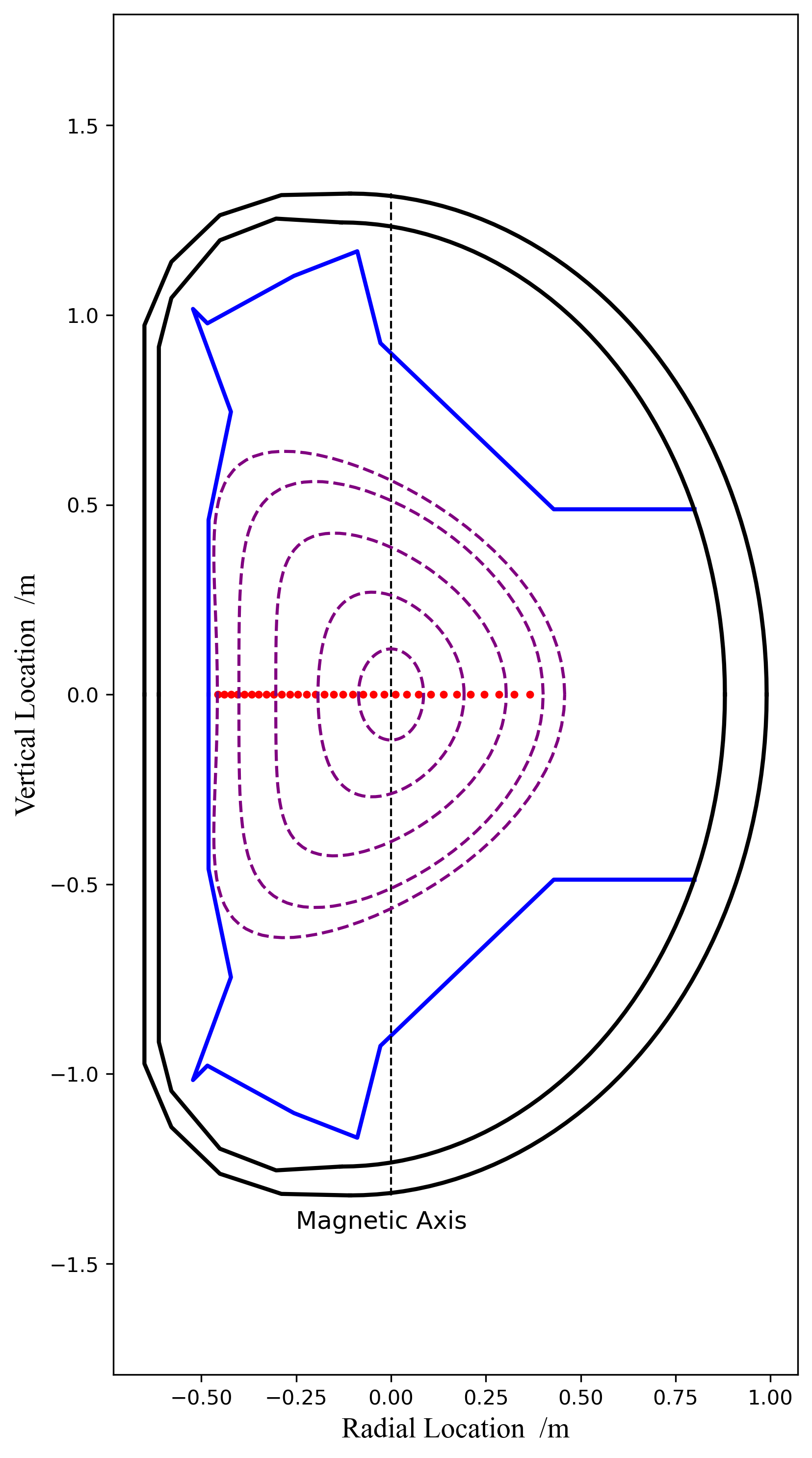

计算部分代码为：

def mcrossection(R0=1.85):
    "将.m文件转写为python"
    ...
def plasma_cross(R0,a,b,kappa,delta,Npol = 100):
    '绘制等离子体截面'
    ...
if __name__ == '__main__':
    e  = 1.602e-19
    me = 9.109e-31

    plt.figure(figsize=(6,12))
    mcrossection()
    
    R0    = 1.85
    B0    = 2.2486
    n     = 2
    gamma = 1
    B_func      = lambda R   : B0*R0/R
    omega_func  = lambda B   : n*e*B/me

    omega_setting = np.arange(105.1,167.1+2,2) * 1e9 #f: GHZ
    observation_points = np.zeros_like(omega_setting)

    # 通过fsolve进行正向解，ω(R)-2πf_target = 0
    for index,omega in enumerate(omega_setting):
        #使用fsolve方法
        R_func = lambda R : omega_func(B_func(R)) - omega*2*np.pi
        observation_points[index] = fsolve(R_func,1.4)
    print(observation_points)
    # 通过公式进行反向解
    observation_points_func = lambda f: n*B0*R0*e/(2*np.pi*me*f)
    observation_points = observation_points_func(omega_setting)
    print(observation_points)

    # 由于R0在截面图中的位置为0，计算的观察点需要对R0修正
    opo = observation_points - R0
    plt.scatter(opo,np.zeros_like(omega_setting),c='red',s=8)

    plasma_cross(0,R0-0.999*observation_points[-1], 0.28,1.4,0.0)
    plasma_cross(0,R0-0.99*observation_points[-5], 0.20,1.4,0)
    plasma_cross(0,R0-0.99*observation_points[-10], 0.15,1.4,0)
    plasma_cross(0,R0-0.99*observation_points[-15], 0.05,1.4,0)
    plasma_cross(0,R0-0.99*observation_points[-25], 0,1.4,0)

    plt.savefig("cross.png",dpi=300,bbox_inches = 'tight') 
    plt.show()

题目三

由轫致辐射推导有效电荷数的诊断原理

韧致辐射是指由自由带电粒子的运动速度发生变化时产生的电磁波辐射。由于等离子体中电子速度远远大于离子速度，通常由电子产生韧致辐射。在高温等离子体中，由于热平衡状态的电子与离子库伦碰撞产生的韧致辐射是一种重要的能量损失过程[1]。

通常讨论韧致辐射时不必考虑物体辐射与电磁波之间的平衡，即等离子体中的总辐射在理想情况下等于每个电子的辐射总和。一个电荷为e的粒子在折射率为n的介质中，以速度为v，加速度为a运动时，辐射功率为

\frac{d E}{d t} = \frac{e^{2} n}{6 π ϵ_{0} c^{3}} \frac{(a)^{2} - (v \times a)^{2} / c^{2}}{(1 - v^{2} / c^{2})^{3}}

忽略相对论效应，辐射功率为

\frac{d E}{d t} = \frac{e^{2} n}{6 π ϵ_{0} c^{3}} a^{2} (t)

辐射能量为：

E = \frac{e^{2} n}{6 π ϵ_{0} c^{3}} \int_{- \infty}^{\infty} a^{2} (t) d t

将a(t)依据傅里叶积分展开，可以得到单一粒子辐射的频谱

E_{ω} d ω = \frac{e^{2} n}{24 π^{2} ϵ_{0} c^{3}} | a (ω) |^{2} d ω

在高温等离子体中，韧致辐射主要来源电子与离子的碰撞过程，假设离子静止，电子在离子的库伦场中受到向心力而做类圆周运动，对于带有电荷量Ze的离子，距离r(t)、质量为m的电子，加速度为：

a = \frac{1}{m} F = \frac{1}{m} \cdot - \frac{Z e^{2}}{4 π ϵ_{0} r^{2} (t)} \frac{r (t)}{r (t)}

当电子运动越来越接近离子时，上述经典力学的方法会失效，需要引入量子力学处理，给出电子温度$T_e$的等离子体在每单位体积中、在频率为$\nu$的单位频率间隔内所发出的辐射功率U_{ν,Te}为

U_{ν, T e} = \frac{N_{e} N_{i} n Z^{2} e^{6}}{3 \sqrt{6} π^{3 / 2} ϵ_{0}^{2} c^{3} m^{3 / 2}} (k T_{e})^{- \frac{1}{2}} \bar{g} \exp (- \frac{h ν}{k T_{e}})

其中g为冈特因子，能够作为量子力学引起的修正因子、并且会随着光子波长以及温度发生变化，一般用来诊断韧致辐射的冈特因子表达式为[2]：

g = \frac{\sqrt{3}}{π} \ln (\frac{k_{B} T_{e}}{h ν})

有效电荷数定义为，若等离子体中仅含有几种离子和电子[3]:

Z_{e f f} = \frac{\sum_{k} n_{k} z_{k}^{2}}{\sum_{k} n_{k} z_{k}} = \frac{\sum_{k} n_{k} z_{k}^{2}}{n_{e}}

使用有效电荷数以替代辐射功率表达式中的Z，并引入准中性条件，观察表达式，发现

U (T e) = c o n s t \cdot Z_{e f f} N_{e}^{2} \sqrt{k T_{e}} [W / m^{3}]

即辐射功率只与有效电荷数、电子温度以及电子密度相关。在诊断时，当确定了系统中的电子温度与电子密度，即可根据韧致辐射功率诊断处等离子体中的有效电荷数。

[1]项志遴.高温等离子体诊断技术[M].上海科学技术出版社,1982.
[2]陈丽. HL-2A装置中轫致辐射诊断及应用[D].电子科技大学,2016.
[3]王龙著. 磁约束等离子体实验物理[M]. 北京：科学出版社, 2018

等离子体诊断方法-第四章：等离子体辐射

等离子体诊断方法-第四章：等离子体辐射

题目一

题目二

题目三

等离子体诊断方法-最终章：实验仿星器装置

等离子体诊断方法-第二章：折射

数值计算三——微分方程组的求解与Modelica

传热学二：利用稀疏矩阵快速求解

评论 (0)