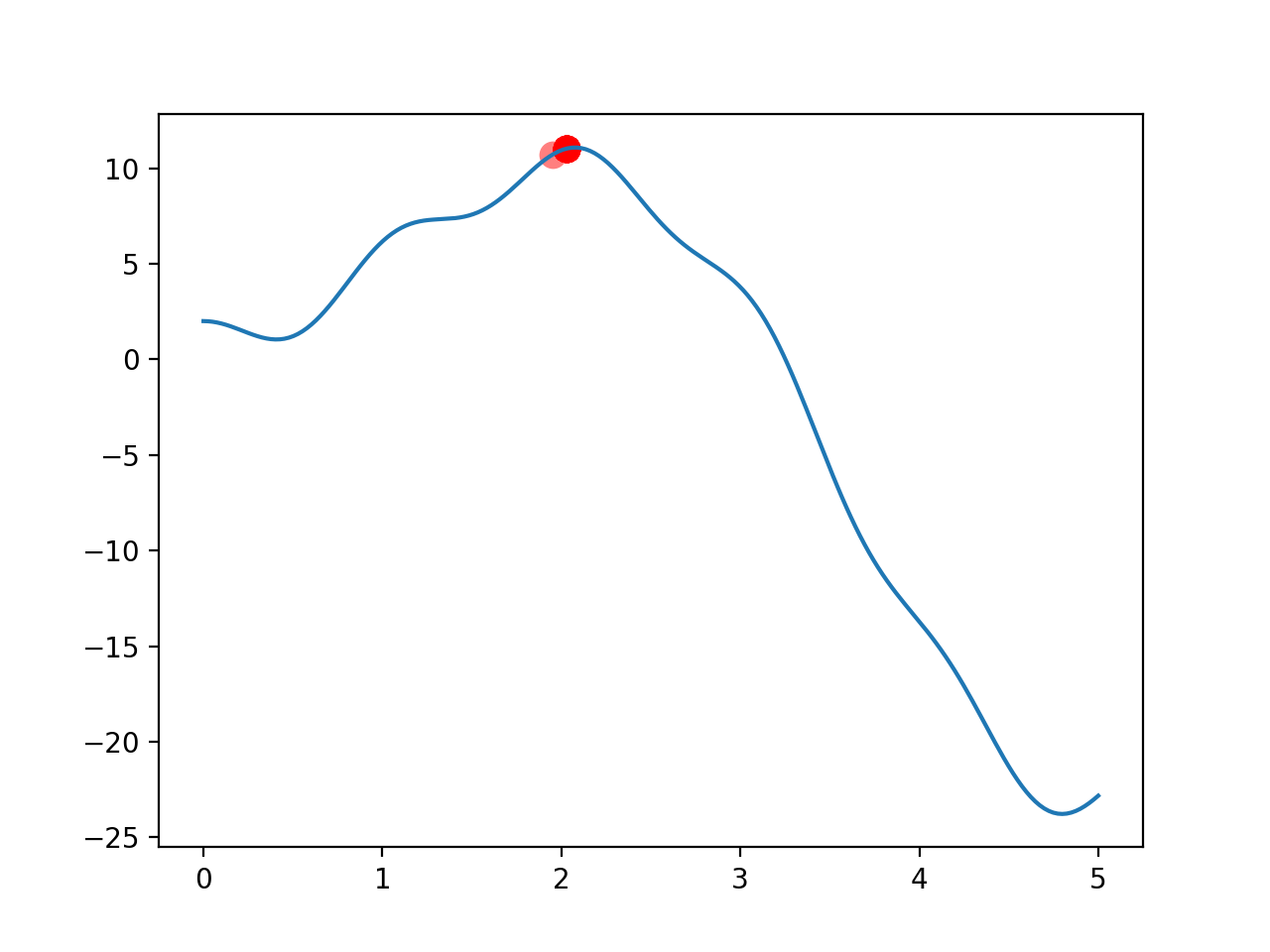
遗传算法学习笔记一：重新发明简易轮子 想起高中，不妨回忆一下生物必修二在记忆中所占的权重。想一想刷遗传题时的痛苦和折磨，想一想减数分裂的框图有多长，生物老师让你默写过多少次减数分裂框图，最后生物必修二内容又能拿多少分。但这些可以是一个有趣的数学问题。为了让一个实际问题变得更容易贴合生物学实际，咱们先从二维函数极值点问题出发，去初步感受一下轮子是怎么变圆的。摘抄自百度百科：“遗传算法（Genetic Algorithm，GA）最早是由美国的 John holland于20世纪70年代提出,该算法是根据大自然中生物体进化规律而设计提出的。是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法。该算法通过数学的方式,利用计算机仿真运算,将问题的求解过程转换成类似生物进化中的染色体基因的交叉、变异等过程。”对于遗传算法，核心有如下几个：1、figness适应度函数2、select选择3、crossover交叉4、mutantion变异这些概念可以十分轻松的在高中生物必修二中发现。这次我们将通过计算机方法去实现这个神奇的过程。因为站在如今人类的知识层级上，遗传算法塑造了我们，还让我们发现了遗传算法。其实我也不太记得人类是不是有丝分裂了，但是减数分裂还是记得的。但无论是何种分裂，核心是生物体的遗传信息存在与DNA中，DNA是携带遗传信息的长链，由四种碱基的不同排列组成了构成了纷繁复杂的生物体，以及他们各自的功能。没有DNA的此种特性，Shakespeare就无法love, write, sigh, pray, sue, and groan。也许DNA是图灵完备的，但是人类已经掌握二进制了，只需要两个数字即可构建如今的数字帝国。因此，进行遗传算法的第一项，就是将待求量二进制化。DNA = np.random.randint(2,size=(DNA_SIZE))此方法可以构建出由0，1组成，长为DNA_SIZE的表征二进制的数组。对于一定数量的种群，对每个种群个体分配DNA序列：#pop(population）为[0，2），popsize个，每个长为dnasize的随机数矩阵 #换言之，即由0，1组成的dna长链，种群中每个个体都不相同。 pop = np.random.randint(2,size=(POP_SIZE, DNA_SIZE)) 对于一个二进制数，它均可对应唯一一个十进制整数。由于用二进制非浮点数表示一个非整数数复杂的。因此我们可以采用一种比例放缩的方法。对于一个八位二进制数，可以对应0-255此256个十进制整数。将此256个数归一化再乘上目标求解区间长度。就可以得到具备一定精确度的取值空间了。这个过程可以看作转译过程，算法为：def translateDNA(pop): return pop.dot(2**np.arange(DNA_SIZE)[::-1])/float(2**DNA_SIZE-1)*X_BOUND[1] 其中，X_BOUND=[0,5]接下来，就可以放心构建算法核心了！对于要求解极大值的函数：def F(x): return np.sin(x)*5*x + np.cos(6*x)+1 构建与之相关的fitness适应函数：def get_figness(Y_values): return Y_values + 1e-5 - np.min(Y_values) # y_i值-所有y构成数组的最小值+定义的无穷小量 #遗传算法中不能出现负数，所以要加上无穷小量这个适应函数表征了某个体与最小适应性个体的差值。由于该问题是极大值问题，因此越大越好。Fitness的值可以表征选择该个体的适应性优劣，并可以在Select选择运算内作为选择个体的概率Select选择：在该环节内，要依据适应性能挑选出较优个体，模拟自然选择过程。将fitness的值传入该模块作为每个个体的选择权重。def select(pop,fitness): #注意random.choice函数：依据概率p在指定数组中选择在指定的数组中随机采样 idx = np.random.choice(np.arange(POP_SIZE),size= POP_SIZE,replace=True, p=fitness/fitness.sum()) return pop[idx] #随机选择种群中都某一个个体，表征个体的是他的dna 选择出来的大概率是适应性高个体，小概率是适应性个体。一时的失败不算是失败，运气也是实力的一部分也许。Crossover交叉环节：实际生物体遗传时，染色体见会发生交叉互换的情况。这里我们简化这种交叉互换，采用随机数的方式随机选择亲本处需要替换的地方。将亲本1的部分序列值由序列2对应部分替换，形成子代。这里用到的算法比较有意思，运用了bool类型在数组中的选择作用。首先我们生产与DNA等长的随机序列，并将其转换为bool类型：cross_points = np.random.randint(0,2,DNA_SIZE).astype(np.bool_) 输出形式为：[ True True False False False False True True False True]对于数组a而言，a[crossover_point]选择了所有bool类型为true的元素；而b[c_p]=a[c_p]就是将a中true的元素赋予b中true元素对应的位置上。进而完成交叉这一行为。def crossover(parent, pop): if np.random.rand()<CROSS_RATE: index = np.random.randint(0,POP_SIZE,size=1) cross_points = np.random.randint(0,2,DNA_SIZE).astype(np.bool_) #corssover的原理是由于cross_point被定义为了布尔类型： #对于数组a而言，a[crossover_point]选择了所有bool类型为true的元素 #b[c_p]=a[c_p]就是将a中true的元素赋予b中true元素对应的位置上。完成交叉。 parent[cross_points]= pop[index, cross_points] return parent mutation 变异：学核科学的，自然知道在辐射条件下基因会发生突变。因此，基因可能会发生良性突变，也可能发生恶性突变，但是总会有几率突变。定义突变机率：MUTATION_RATE = 0.003 def mutation(child): for point in range(DNA_SIZE): if np.random.rand()< MUTATION_RATE: if child[point] == 1: child[point] = 0 else: child[point]=1 return child （注意结合主循环内内容，之后会展示，此时，child已经变成一个体了）到此为止，我们已经得到了构成一个普通遗传算法的几个关键函数。接下来构建主函数，连接起各核心功能；流程图如下，图片抄自百度百科：定义种群生长代数：GENERATIONS=200对于每代种群：1、获取目标函数值：F_value = F(translateDNA(pop))2、获取个体适应度fitness = get_figness(F_value)3、Select选择：依据适应度选择多个个体并填充全部种群pop = select(pop,fitness)创建另一个亲本，采用复制的方式pop_copy=pop.copy()4、对于每一个个体与其另一亲本进行crossover交叉配对，且随之变异for parent in pop: child = crossover(parent,pop_copy) child = mutation(child) parent[:] = child #完整复制一遍,同时更改了pop本身 完整代码如下：import numpy as np import matplotlib.pyplot as plt DNA_SIZE = 20 X_BOUND=[0,5] POP_SIZE = 10 CROSS_RATE= 0.8 MUTATION_RATE = 0.003 GENERATIONS = 200 #GA作用的目标函数 def F(x): return np.sin(x)*5*x + np.cos(6*x)+1 #GA的核心：fitness适应度，评价子代的指标。 def get_figness(Y_values): return Y_values + 1e-5 - np.min(Y_values) # y_i值-所有y构成数组的最小值+定义的无穷小量 #遗传算法中不能出现负数 #在范围内将x编码成二进制数，并且将二进制数缩放到所需要的范围内。 #pop（population）是一个储存二进制DNA的矩阵，形状与POP_SIZE和DNA_SIZE相关。 #pop.dot(2**xxx)的部分实际上是利用数权法进行2-10进制转换；.dot是返回两个向量内积 def translateDNA(pop): return pop.dot(2**np.arange(DNA_SIZE)[::-1])/float(2**DNA_SIZE-1)*X_BOUND[1] ''' 进化的三要素：选择：select；交叉：crossover；变异：mutation ''' #第一步，选择 def select(pop,fitness): #注意random.choice函数：依据概率p在指定数组中选择在指定的数组中随机采样 idx = np.random.choice(np.arange(POP_SIZE),size= POP_SIZE,replace=True, p=fitness/fitness.sum()) return pop[idx] #随机选择种群中某一类个体并替换全部个体，选择后种群内个体几乎是适应性强的，表征个体的是他的dna #第二步，交叉配对 def crossover(parent, pop): if np.random.rand()<CROSS_RATE: index = np.random.randint(0,POP_SIZE,size=1) cross_points = np.random.randint(0,2,DNA_SIZE).astype(np.bool_) #corssover的原理是由于cross_point被定义为了布尔类型： #对于数组a而言，a[crossover_point]选择了所有bool类型为true的元素 #b[c_p]=a[c_p]就是将a中true的元素赋予b中true元素对应的位置上。完成交叉。 parent[cross_points]= pop[index, cross_points] return parent #第三步，变异 #child在主循环里已经定义为pop内的某一个体，因此只需要考虑dna上有多少基因需要突变即可。 def mutation(child): for point in range(DNA_SIZE): if np.random.rand()< MUTATION_RATE: if child[point] == 1: child[point] = 0 else: child[point]=1 return child if __name__ == "__main__": #pop(population）为[0，2），popsize个，每个长为dnasize的随机数矩阵 #换言之，即由0，1组成的dna长链，种群中每个个体都不相同。 pop = np.random.randint(2,size=(POP_SIZE, DNA_SIZE)) plt.ion() x=np.linspace(*X_BOUND,200) plt.plot(x,F(x)) for flag in range(GENERATIONS): F_value = F(translateDNA(pop)) if 'sca' in globals(): sca.remove() sca = plt.scatter(translateDNA(pop), F_value, s=100,lw=0 , c='red',alpha=0.5);plt.pause(0.01) fitness = get_figness(F_value) pop = select(pop,fitness) pop_copy=pop.copy() #为产生子代而人为备份亲本 pop1 = pop for parent in pop: child = crossover(parent,pop_copy) child = mutation(child) parent[:] = child #完整复制一遍，同时改变了pop本身。 print('\r',flag,"/",GENERATIONS,end='', flush=True) print('\n',child) print(translateDNA(pop)) plt.ioff(); plt.show()结果如图所示：

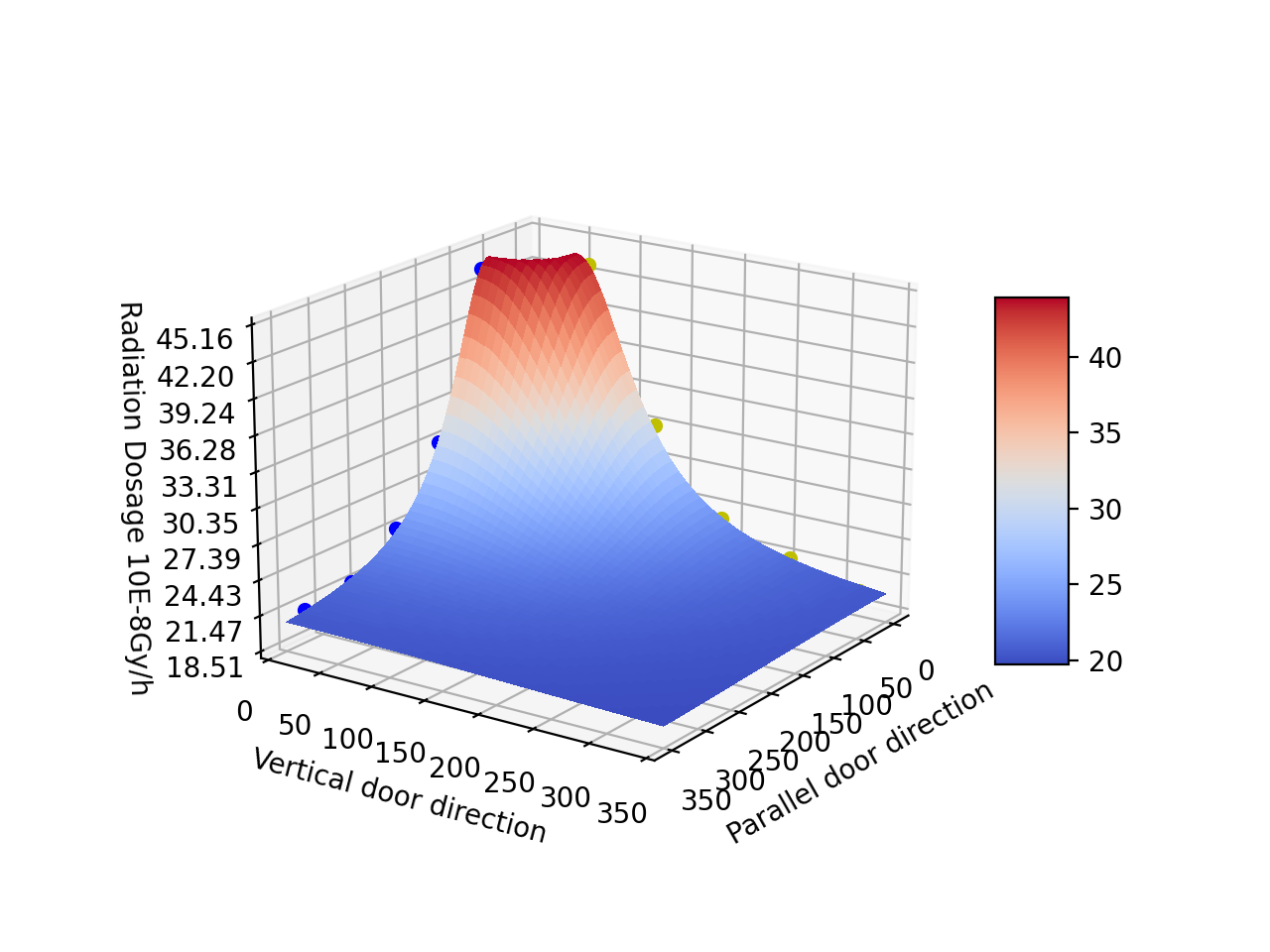
辐射实验数据处理一：通过有限点绘制曲面图 首先吐槽一下这种为了赶进度而在尚未学习核物理与辐射安全前就做实验的行为；在实验六：环境伽马剂量监测实验中，要求绘制指定放射源的剂量分布图谱，但受制于实验场地，只能测量横纵两个相互垂直方向共十组数据。但实验同时要求我们使用软件绘制剂量分布的三维图像。显然已由的这些垂直的点放到Matlab里出来的是简单的平面堆叠。为此，需要找到一种方法绘制出优美的曲面出来。当然，这和学习无关，和得分无关。纯粹是个人爱好。首先，检查python和相关库，这里用的是python3.8 + matplotlib + scipy + numpy，都是很基础的库。不会pip方法的可以用Anaconda3一键安装。接下来，需要对原始数据进行处理。纵向平均值纵向平均值65  43.26543.1513029.813030.5019524.0519523.7026021.2526021.6032520.7532520.10这些点在空间中的样子是这样的：怎么画出来？代码如下：from mpl_toolkits.mplot3d import Axes3D import matplotlib.pyplot as plt import numpy as np fig = plt.figure() ax = fig.add_subplot(111, projection='3d') #scatter就是描点命令，s是点的大小，c是点的颜色。需要复现的无脑改数据就完事了。 ax.scatter(65, 0, 43.2, s=20, c='r', depthshade=True) ax.scatter(130, 0, 29.8, s=20, c='r', depthshade=True) ax.scatter(195, 0, 24.05, s=20, c='r', depthshade=True) ax.scatter(260, 0, 21.25, s=20, c='r', depthshade=True) ax.scatter(325, 0, 20.75, s=20, c='r', depthshade=True) ax.scatter( 0, 65,43.15, s=20, c='b', depthshade=True) ax.scatter( 0, 130,30.5, s=20, c='b', depthshade=True) ax.scatter( 0, 195,23.7, s=20, c='b', depthshade=True) ax.scatter( 0,260, 21.6, s=20, c='b', depthshade=True) ax.scatter( 0, 325,20.1, s=20, c='b', depthshade=True) ax.set_xlabel('Parallel door direction') ax.set_ylabel('Vertical door direction') ax.set_zlabel('Radiation Dosage 10E-8Gy/h') plt.show()核心思路是： 辐射场的分布在空间内是均匀的，因此在xz和yz平面上的曲线符合该场在任意过z轴截面的曲线沿着这个思路，我们需要找到一种方法，寻找出符合该平面上辐射随距离衰减的方式。通过阅读课本和实验手册，我们知道了这个衰减是与距离的平方呈反比的。为此，我打算直接采用最小二乘法拟合出过这些点的曲线。为了令这种拟合变得更加符合实验，我特定选取了如下拟合函数： y=a1/(a2*(x*x)+a3*x+a4) +a5由于换的MBP只有可怜的256g，为此不想在下载Oringin或者Matlab这类软件出拟合曲线了。Python也可以实现，毕竟他们都是图灵完备的。具体实现的方法参照如下代码：import matplotlib.pyplot as plt from scipy.optimize import leastsq import numpy as np def Fun(p, x): # 定义拟合函数形式，这这里定义需要拟合的函数形式 a1,a2,a3,a4,a5 = p #注意p是一个五维列表，最好用np.p的形式，会避免怪错 y=a1/(a2*(x*x)+a3*x+a4) +a5 return y def error(p, x, y): # 拟合残差 return Fun(p, x) - y def main(): x = np.array([65.,130.,198.,260.,325.,1000.]) #输入你的实验数据，注意最后的1000是为了接近本底辐射 y = np.array([43.2,30.,23.9,21.4,20.4,19.45]) #输入你的实验测得的辐射值 p0 = [0.1,0.1,0.1,1,10] # 拟合的初始参数设置 para = leastsq(error, p0, args=(x, y)) # 进行拟合 y_fitted = Fun(para[0], x) # 画出拟合后的曲线 plt.figure plt.plot(x, y, 'r', label='Original curve') plt.plot(x, y_fitted, '-b', label='Fitted curve') plt.legend() plt.show() print(para[0]) if __name__ == '__main__': main()点击运行，不出意外的话会产生如下曲线：是不是很接近？但需要注意的是这个曲线不是非常光滑，因为我懒得写了。同样，也会给出拟合函数的五个未知参数大小： [-1.50903395e+09 -1.30671680e+04 1.38404720e+06 -9.74987756e+07 1.91459819e+01]这样，我就得到了一个漂亮的曲线： Z = (-1.50903395e+09) / ((-1.30671680e+04) * (X * X) + (1.38404720e+06) * X + (-9.74987756e+07)) + (1.91459819e+01);他是长成这样的：这也就是我们要求的距离防护曲线。最后一步就是绘制表面图了。这很简单，觉得难是因为大一的线性代数第二章空间几何没有好好听好好学。已知X-Z图这么绘制绕Z轴旋转的图？将X替换为根号下X的平方+Y的平方！（我讨厌web，我写不了公式）就像这个： Z = (-1.50903395e+09) / ((-1.30671680e+04) * (X * X+Y*Y) + (1.38404720e+06) * np.sqrt(X * X+Y*Y) + (-9.74987756e+07)) + (1.91459819e+01)代码在这里：from mpl_toolkits.mplot3d import Axes3D import matplotlib.pyplot as plt from matplotlib import cm from matplotlib.ticker import LinearLocator, FormatStrFormatter import numpy as np fig = plt.figure() ax = plt.axes(projection='3d') #这一片是把一开始的点描出来明白不？ ax.scatter(65, 0, 43.2, s=20, c='b', depthshade=True) ax.scatter(130, 0, 29.8, s=20, c='b', depthshade=True) ax.scatter(195, 0, 24.05, s=20, c='b', depthshade=True) ax.scatter(260, 0, 21.25, s=20, c='b', depthshade=True) ax.scatter(325, 0, 20.75, s=20, c='b', depthshade=True) ax.scatter( 0, 65,43.15, s=20, c='y', depthshade=True) ax.scatter( 0, 130,30.5, s=20, c='y', depthshade=True) ax.scatter( 0, 195,23.7, s=20, c='y', depthshade=True) ax.scatter( 0,260, 21.6, s=20, c='y', depthshade=True) ax.scatter( 0, 325,20.1, s=20, c='y', depthshade=True) # Make data.这里是XY的取值范围和步长 X = np.arange(0, 350, 0.25) Y = np.arange(0, 350, 0.25) X, Y = np.meshgrid(X, Y) #这里你Matlab肯定见过 Z = (-1.50903395e+09) / ((-1.30671680e+04) * (X * X+Y*Y) + (1.38404720e+06) * np.sqrt(X * X+Y*Y) + (-9.74987756e+07)) + (1.91459819e+01)#这是之前的函数 # Plot the surface. surf = ax.plot_surface(X, Y, Z, cmap=cm.coolwarm, linewidth=0, antialiased=False) # Customize the z axis. ax.set_ylim(0, 350)#注意跳针范围 ax.zaxis.set_major_locator(LinearLocator(10)) ax.zaxis.set_major_formatter(FormatStrFormatter('%.02f')) # Add a color bar which maps values to colors. fig.colorbar(surf, shrink=0.5, aspect=5) ax.set_xlabel('Parallel door direction')#可以添加标签 ax.set_ylabel('Vertical door direction') ax.set_zlabel('Radiation Dosage 10E-8Gy/h') plt.show()点击运行他应该不会报错，这样以来，就会得到这样的美丽图像： 美丽漂亮，还有被隐藏起来的瑕疵。

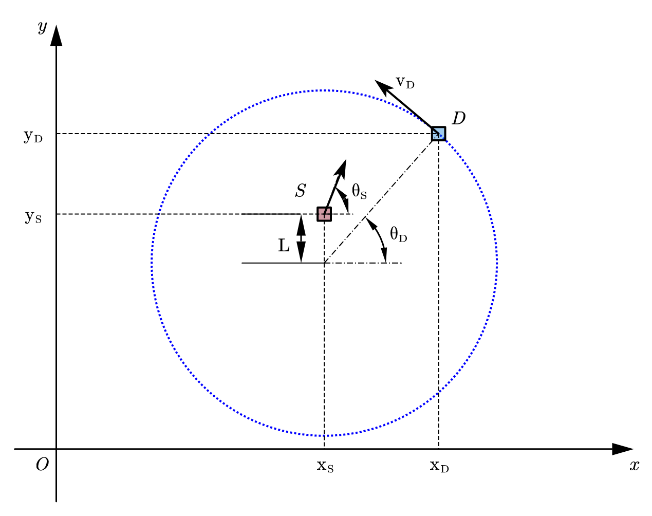
DDPG算法在羊犬博弈中的简要应用 1. 模型的建立与求解 1.1 机器学习方法：DDPG方法 1.1.1 追逃博弈模型 　在该羊犬博弈场景中，羊作为逃跑者，犬作为追捕者。在限制条件下两者具有相反的目的，即羊需要躲避犬并逃出特定区域，犬需要在特定区域内捕获到羊。依次建立的追逃模型如下图所示： 　其中，S为逃跑者，D为追捕者；v_S为逃跑者的线速度大小；v_D为追捕者的线速度大小。θ_S为逃跑者速度方向角，θ_D为追捕者位置与圆心所夹角。 　逃跑者与追捕者的运动学模型为： 　其中，i表示S逃跑者，D追捕者；(x,y)为两者位置；θ是方向，u是转向角。 　需要注意的是，犬（追逃者）的运动方式是固定的，而羊的运动方式是需要通过方法确定的。1.1.2 强化学习方法 　一个马尔科夫决策过程（MDP）可以通过一个五元组(S,A,T,R,γ)描述，该五元组包含了有限状态空间S，有限行为空间A，状态转移函数T，回报函数R与折扣因子γ。状态转移函数表示了下一时刻状态是依据何种概率分布从当前状态进行转移的。回报函数则描述了当前状态下可以为下一状态提供的回报。对于任意马尔科夫决策过程，描述对象都存在一个确定的最优策略。因而选择一种合适的机器学习方法是解决该博弈问题的关键。依据该模型依赖的过程：对象行为作用于环境并且从环境取得回报，明确了应当采用一种强化学习方法。 1.1.3 基于DDPG的算法 　针对该博弈模型中描述对象行为为连续动作，考虑到学习效率，采用深度学习中的DDPG算法，定义MDP状态空间与行为空间，设计回报函数，进而实现逃脱者的控制算法，引导逃脱者在躲避追捕者的前提下逃出特定范围。 给定MDP状态空间： 　羊（逃脱者）的策略由强化学习给出，狼的状态固定。动作空间可定为： 　其MDP转移函数即为上述运动学方程： 　回报函数给定为： 　DDPG算法是由Google DeepMind 提出的一种使用Actor-Critic结构, 但是输出的不是行为的概率, 而是具体的行为, 用于连续动作 (continuous action) 的预测。可以提高Actor-Critic的稳定性和收敛性。　Actor网络输出动作对象的行为策略，Critic网络输出对该行为的评估。　Critic网络代价函数如下： 　其中： 　借鉴了DQN和Double Q learning的方式。　Actor网路的策略梯度为： 1.1.4.追逃博弈算法 1.1.5.算法验证 1.1.5.1 参数设置 　在python语言环境下，以深度学习框架TensorFlow为基础，隐藏层数为2；算法使用minibatch大小为32，经验池大小为6000，actor学习率为0.001，critic学习率为0.001，折扣因子为0.9，soft replacement设置为0.01。其它实验参数如表所示 1.1.5.2.结果分析 　训练时，追捕者犬做可变方向的匀速圆周运动，且会随着羊的运动而不断向羊趋近。经过若干次实验，在算法训练10000次下，记录累计回报。如图所示。算法在500次左右时开始收敛，在1000次内存在一个小幅抖动。对于算法整体10000次的回报情况，如下图所示。不难发现，该算法随着训练次数的增加，并不能够稳定的收敛在一个值上。 　　图1 1000次训练内EPSISODES-REWARD关系 　　图2 10000次训练EPSISODES-REWARD关系　考察每次训练时单次训练于完成训练步长。可以得到如下所示图。该图反应了在算法接近稳定后，存在一个稳定在75步长完成一次训练的趋势。 　图3 10000次训练EPSISODES-STEP关系　通过导出经过上述过程训练后模型逃逸成功的位置数据，可以直观的描绘出在该初始条件下收敛处的最优逃出路线以及未训练前羊狼运动的轨迹。 　图4 训练前某次训练羊犬运动路径 　图5 训练后羊逃逸最优路径　对比每次训练时奖励与步长的变化关系，不难发现在该算法目前设置下存在收敛不充分的情况。而这正是Policy Gradient算法自身存在的缺陷。 Policy Gradient会受Learning rate 或 Step size影响，会产生收敛不充分或者时间过长的缺点。而该算法产生缺点的原因，正是此前PPO算法优化和避免的部分。附录：代码#main.py # tensorflow == 1.2.1 # pyglet == 1.2.4 # xlsxwriter == 3.0.1 # numpy == 1.19.5 # gym == 0.18.3 import numpy as np from test import SDEnv from rl import DDPG import xlsxwriter as xw workbook=xw.Workbook('list.xlsx') worksheet = workbook.add_worksheet('sheet1') headings=['EPSISODES','STEP','REWARD'] MAX_EPISODES = 10000 MAX_EP_STEPS = 300 ON_TRAIN = False a1=np.zeros(MAX_EPISODES) a2=np.zeros(MAX_EPISODES) a3=np.zeros(MAX_EPISODES) # set env env = SDEnv() s_dim = env.state_dim a_dim = env.action_dim a_bound = env.action_bound # set RL method (continuous) rl = DDPG(a_dim, s_dim, a_bound) steps = [] def train(): # start training for i in range(MAX_EPISODES): s = env.reset() ep_r = 0. a1[i]=i for j in range(MAX_EP_STEPS): env.render() a = rl.choose_action(s) s_, r, done = env.step(a) rl.store_transition(s, a, r, s_) ep_r += r if rl.memory_full: # start to learn once has fulfilled the memory rl.learn() s = s_ if done or j == MAX_EP_STEPS-1: a2[i]=j a3[i]=ep_r print('Ep: %i | %s | ep_r: %.1f | step: %i' % (i, '---' if not done else 'done', ep_r, j)) break list = [a1, a2, a3] worksheet.write_row('A1',headings) worksheet.write_column('A2',list[0]) worksheet.write_column('B2', list[1]) worksheet.write_column('C2', list[2]) workbook.close() rl.save() def eval(): rl.restore() env.render() env.viewer.set_vsync(True) while True: s = env.reset() for _ in range(200): env.render() a = rl.choose_action(s) s, r, done = env.step(a) if done: break if ON_TRAIN: train() else: eval()#test.py import pyglet import numpy as np pyglet.clock.set_fps_limit(10000) class Viewer(pyglet.window.Window): bar_thc=4 #羊的宽度 def __init__(self,sheep_info,dog_info,i): super(Viewer,self).__init__(width=400,height=400,resizable=False,caption='sheep',vsync=False) #背景颜色 pyglet.gl.glClearColor(1,1,1,1) #将羊的信息放入到batch内 self.batch = pyglet.graphics.Batch() self.sheep_info = sheep_info self.center_coord= np.array([200,200]) self.dog_info = dog_info self.i=i #添加羊的信息 self.sheep = self.batch.add( 4, pyglet.gl.GL_QUADS, None, ('v2f',[200,200, 200,204, 204,204, 204,200]), ('c3B',(86,109,249)*4)) #添加犬的信息 dx,d1=self.dog_info['x'] dy,d2=self.dog_info['y'] dl,d3=self.dog_info['l'] self.dog = self.batch.add( 4, pyglet.gl.GL_QUADS, None, ('v2f', [dx - dl / 2, dy - dl / 2, dx - dl / 2, dy + dl / 2, dx + dl / 2, dy + dl / 2, dx + dl / 2, dy - dl / 2]), ('c3B', (249, 86, 86) * 4)) def render(self): self._update_sheep() self.switch_to() self.dispatch_events() self.dispatch_event('on_draw') self.flip() def on_draw(self): self.clear() # 清屏 self.batch.draw() # 画上 batch 里面的内容 def _update_sheep(self): sx,s1=self.sheep_info['x'] sy,s2=self.sheep_info['y'] sr,s23=self.sheep_info['r'] sxy=self.center_coord sxy_=np.array([sx,sy]) xy01 =sxy+ np.array([sx + self.bar_thc / 2, sy + self.bar_thc / 2]) xy02 =sxy + np.array([sx + self.bar_thc / 2, sy - self.bar_thc / 2]) xy11 =sxy+ np.array([sx - self.bar_thc / 2, sy - self.bar_thc / 2]) xy12 = sxy+ np.array([sx - self.bar_thc / 2, sy + self.bar_thc / 2]) self.sheep.vertices = np.concatenate((xy01,xy02,xy11,xy12)) dx, d1 = self.dog_info['x'] dy, d2 = self.dog_info['y'] dl, d3 = self.dog_info['l'] self.dog.vertices=[dx - dl / 2, dy - dl / 2, dx - dl / 2, dy + dl / 2, dx + dl / 2, dy + dl / 2, dx + dl / 2, dy - dl / 2] print(sx,sy,dx,dy) class SDEnv(object): viewer = None dt = 0.1 # 转动的速度和 dt 有关 action_bound = [-1, 1] # 转动的角度范围 i = 0 #dog = {'x': x_dog, 'y': y_dog, 'l': 4} # 蓝色 dog 的 x,y 坐标和长度 l state_dim = 2 # 两个观测值 action_dim = 2 # 两个动作 def __init__(self): self.sheep_info = np.zeros( 2,dtype=[('x',np.float32),('y',np.float32),('r',np.float32),]) #生成一届矩阵 self.sheep_info['x'] = 1 self.sheep_info['y'] = 1 self.sheep_info['r'] = 0 #羊开始是速度方向角 self.dog_info= np.zeros( 2,dtype=[('x',np.float32),('y',np.float32),('R',np.float32),('v',np.float32),('l',np.float32),('r',np.float32)]) self.dog_info['x']=350 self.dog_info['y']=200 self.dog_info['R']=150 self.dog_info['v']=30 self.dog_info['l']=4 self.dog_info['r'] = 0 def render(self): if self.viewer is None: self.viewer = Viewer(self.sheep_info,self.dog_info,self.i) self.viewer.render() def step(self,action): done = False r = 0 v_sheep = 20 self.i += 1 before1,before11=self.sheep_info['x'] before2,before22=self.sheep_info['y'] if self.sheep_info['x'][0] < 0: if self.sheep_info['y'][0] > 0: srr = np.pi + np.arctan(self.sheep_info['y'][0] / self.sheep_info['x'][0]) else: srr = -np.pi + np.arctan(self.sheep_info['y'][0] / self.sheep_info['x'][0]) else: srr = np.arctan(self.sheep_info['y'][0] / self.sheep_info['x'][0]) drr,drrr=self.dog_info['r'] if srr>=drr: self.dog_info['r'] += (self.dog_info['v'] / self.dog_info['R']) * self.dt else: self.dog_info['r'] -= (self.dog_info['v'] / self.dog_info['R']) * self.dt self.dog_info['x'] = self.dog_info['R'] * np.cos(self.dog_info['r']) + 200 self.dog_info['y'] = self.dog_info['R'] * np.sin(self.dog_info['r']) + 200 #print(self.dog_info['x']) if self.sheep_info['x'][0] > 0: if self.sheep_info['y'][0] > 0: srrr = np.arctan(self.sheep_info['y'][0] / self.sheep_info['x'][0]) else: srrr = 2*np.pi + np.arctan(self.sheep_info['y'][0] / self.sheep_info['x'][0]) else: srrr = np.pi + np.arctan(self.sheep_info['y'][0] / self.sheep_info['x'][0]) action= np.clip(action,*self.action_bound) self.sheep_info['r'] += action*self.dt self.sheep_info['r'] %= 2 * np.pi self.sheep_info['x'] += v_sheep * np.cos(self.sheep_info['r'] ) * self.dt #self.sheep_info['x'] %= 150 self.sheep_info['y'] += v_sheep * np.sin(self.sheep_info['r'] ) * self.dt #self.sheep_info['y'] %= 150 s=self.sheep_info['r'] sx,s2 = self.sheep_info['x'] sy,s21 = self.sheep_info['y'] sr,s22 = self.sheep_info['r'] sxy = np.array([sx,sy]) finger = sxy+np.array([200.,200.]) dx, d1 = self.dog_info['x'] dy, d2 = self.dog_info['y'] dl, d3 = self.dog_info['l'] #print(sx*sx+sy*sy-150*150) if sx*sx+sy*sy < before1*before1+before2*before2: r=-101 #done = True if 148 * 148 < sx * sx + sy * sy < 152 * 152 : self.sheep_info['x'] = 1 self.sheep_info['y'] = 1 self.dog_info['r'] = 0 if (sx+200-dx)**2+(sy+200-dy)**2>4: done = True r = 100 else: done = True r = -100 return s, r, done def reset(self): self.sheep_info['r']=2*np.pi*np.random.rand(2) return self.sheep_info['r'] def sample_action(self): return np.random.rand(2)-0.5 if __name__ == '__main__': env = SDEnv() while True: env.render() env.step(env.sample_action()) #rl.py import tensorflow as tf import numpy as np ##################### hyper parameters #################### LR_A = 0.001 # learning rate for actor LR_C = 0.001 # learning rate for critic GAMMA = 0.9 # reward discount TAU = 0.01 # soft replacement MEMORY_CAPACITY = 60000 BATCH_SIZE = 32 class DDPG(object): def __init__(self, a_dim, s_dim, a_bound,): self.memory = np.zeros((MEMORY_CAPACITY, s_dim * 2 + a_dim + 1), dtype=np.float32) self.pointer = 0 self.memory_full = False self.sess = tf.Session() self.a_replace_counter, self.c_replace_counter = 0, 0 self.a_dim, self.s_dim, self.a_bound = a_dim, s_dim, a_bound[1] self.S = tf.placeholder(tf.float32, [None, s_dim], 's') self.S_ = tf.placeholder(tf.float32, [None, s_dim], 's_') self.R = tf.placeholder(tf.float32, [None, 1], 'r') with tf.variable_scope('Actor'): self.a = self._build_a(self.S, scope='eval', trainable=True) a_ = self._build_a(self.S_, scope='target', trainable=False) with tf.variable_scope('Critic'): # assign self.a = a in memory when calculating q for td_error, # otherwise the self.a is from Actor when updating Actor q = self._build_c(self.S, self.a, scope='eval', trainable=True) q_ = self._build_c(self.S_, a_, scope='target', trainable=False) # networks parameters self.ae_params = tf.get_collection(tf.GraphKeys.GLOBAL_VARIABLES, scope='Actor/eval') self.at_params = tf.get_collection(tf.GraphKeys.GLOBAL_VARIABLES, scope='Actor/target') self.ce_params = tf.get_collection(tf.GraphKeys.GLOBAL_VARIABLES, scope='Critic/eval') self.ct_params = tf.get_collection(tf.GraphKeys.GLOBAL_VARIABLES, scope='Critic/target') # target net replacement self.soft_replace = [[tf.assign(ta, (1 - TAU) * ta + TAU * ea), tf.assign(tc, (1 - TAU) * tc + TAU * ec)] for ta, ea, tc, ec in zip(self.at_params, self.ae_params, self.ct_params, self.ce_params)] q_target = self.R + GAMMA * q_ # in the feed_dic for the td_error, the self.a should change to actions in memory td_error = tf.losses.mean_squared_error(labels=q_target, predictions=q) self.ctrain = tf.train.AdamOptimizer(LR_C).minimize(td_error, var_list=self.ce_params) a_loss = - tf.reduce_mean(q) # maximize the q self.atrain = tf.train.AdamOptimizer(LR_A).minimize(a_loss, var_list=self.ae_params) self.sess.run(tf.global_variables_initializer()) def choose_action(self, s): return self.sess.run(self.a, {self.S: s[None, :]})[0] def learn(self): # soft target replacement self.sess.run(self.soft_replace) indices = np.random.choice(MEMORY_CAPACITY, size=BATCH_SIZE) bt = self.memory[indices, :] bs = bt[:, :self.s_dim] ba = bt[:, self.s_dim: self.s_dim + self.a_dim] br = bt[:, -self.s_dim - 1: -self.s_dim] bs_ = bt[:, -self.s_dim:] self.sess.run(self.atrain, {self.S: bs}) self.sess.run(self.ctrain, {self.S: bs, self.a: ba, self.R: br, self.S_: bs_}) def store_transition(self, s, a, r, s_): transition = np.hstack((s, a, [r], s_)) index = self.pointer % MEMORY_CAPACITY # replace the old memory with new memory self.memory[index, :] = transition self.pointer += 1 if self.pointer > MEMORY_CAPACITY: # indicator for learning self.memory_full = True def _build_a(self, s, scope, trainable): with tf.variable_scope(scope): net = tf.layers.dense(s, 100, activation=tf.nn.relu, name='l1', trainable=trainable) a = tf.layers.dense(net, self.a_dim, activation=tf.nn.tanh, name='a', trainable=trainable) return tf.multiply(a, self.a_bound, name='scaled_a') def _build_c(self, s, a, scope, trainable): with tf.variable_scope(scope): n_l1 = 100 w1_s = tf.get_variable('w1_s', [self.s_dim, n_l1], trainable=trainable) w1_a = tf.get_variable('w1_a', [self.a_dim, n_l1], trainable=trainable) b1 = tf.get_variable('b1', [1, n_l1], trainable=trainable) net = tf.nn.relu(tf.matmul(s, w1_s) + tf.matmul(a, w1_a) + b1) return tf.layers.dense(net, 1, trainable=trainable) # Q(s,a) def save(self): saver = tf.train.Saver() saver.save(self.sess, './params', write_meta_graph=False) def restore(self): saver = tf.train.Saver() saver.restore(self.sess, './params')

WKB近似方法在一维量子力学体系中的推导与应用 简单推导了WKB近似方法以及具体应用