搜索到
2
篇与
核工程
的结果
-

-
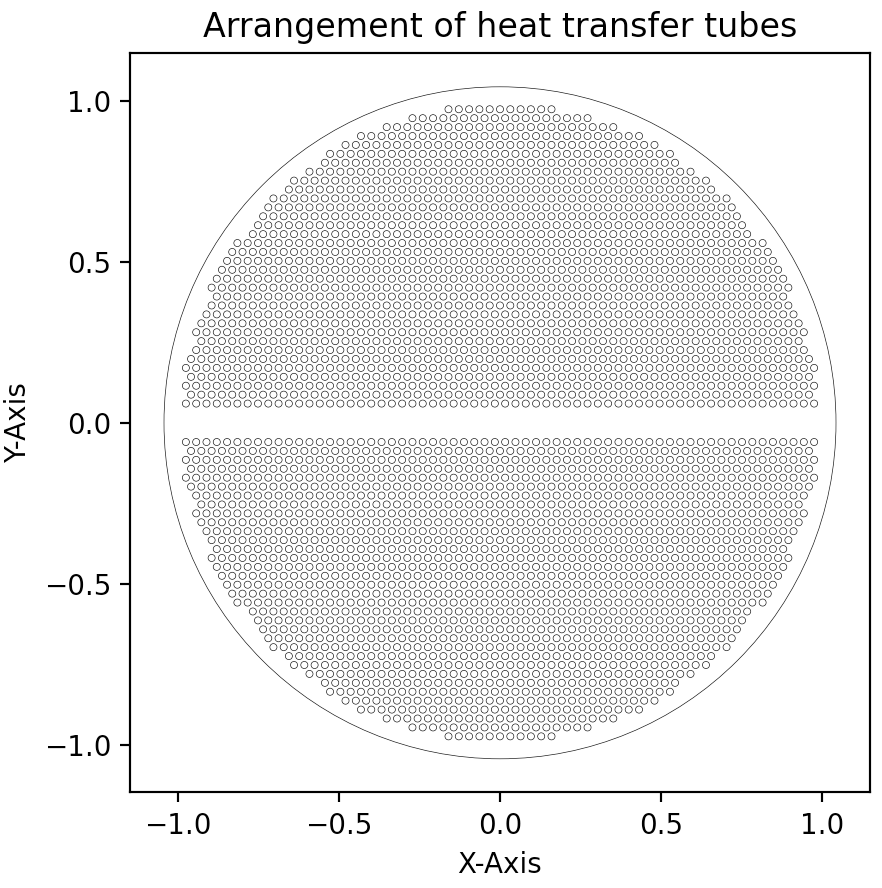
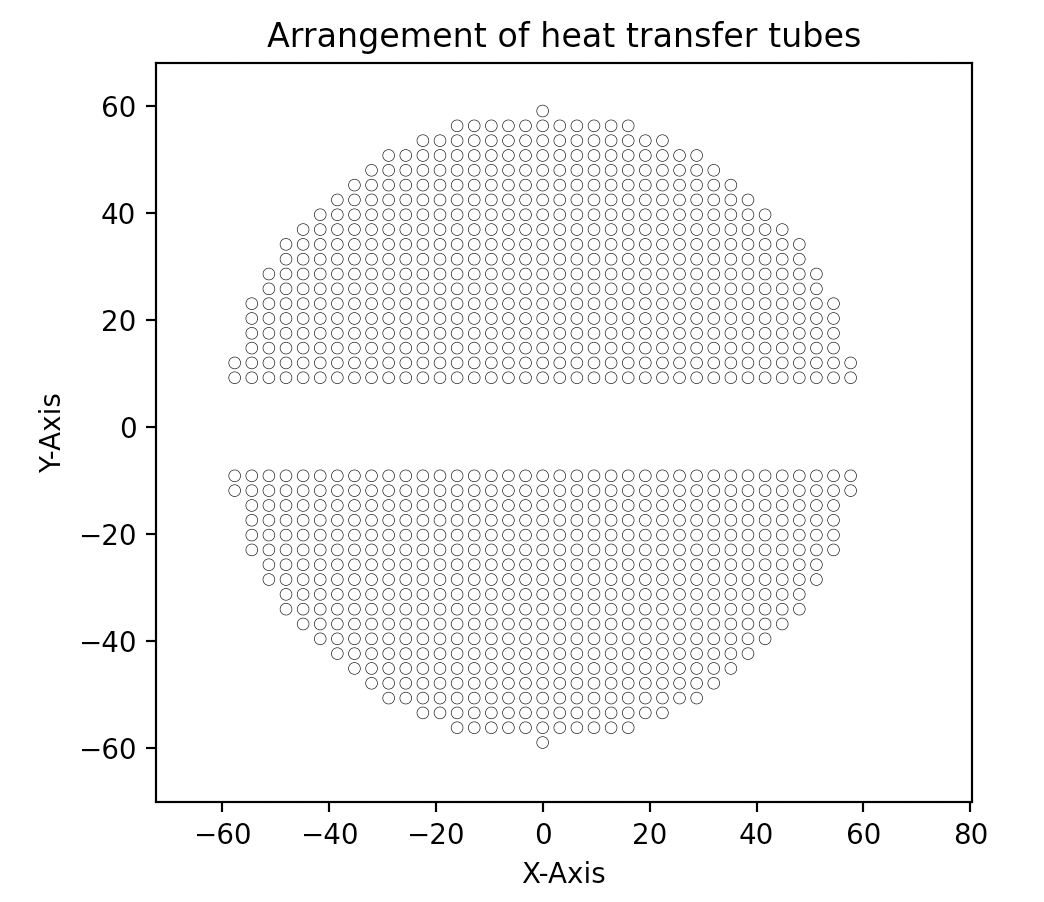
 换热器排管助手V0.9:极低运行效率下的换热器排管及绘制 项目源起大三下学期,涉及了两个关于换热器的课程设计&核动力设备大作业,不出意外,过段时间的课设三也是直立式蒸汽发生器。无论在课设还是大作业,排管始终是一个令人头疼的问题。课设中1.1倍根号下总管数确定中心管数属实令人费解(考虑优化的时候知道是怎么回事了)。核动力设备大作业中也因为没有合理的排布(类圆形)而被老师批评。对于数百个乃至数千根管,如何快速、简便、合理的绘制成了萦绕在我心头解不开的问题。于是从暑假拖到了现在。程序目标程序将要实现:对于给定的管间距参数,在任意排管方式(正方形、正三角形)下,对于任意的管数N,都能够给出一种排布方式及其排布图。且能够被其它程序方便引用。设计思路由于编者能力水平低下,此篇文章中,将介绍一种目前效率极其低下但容易实现的思路。依据排布要求,对于总数N,生成第一象限中(含坐标轴)范围为(N,N)的圆心位置。假定一个半径为R的圆,遍历所有圆心位置,取出所有在圆内且满足边界条件的圆心位置。计算R下符合条件的圆心位置数量是否近似满足总管数在第一象限分布的数量。若不满足,则令R递增,直至满足为止。坐标变换,通过第一象限的点生产全象限的完整分布绘制排布图。思路非常暴力,非常简单,非常低效。但是正在优化,有了初步思路。程序设计总览为了便于调用,整个排布图将设计为类形式,它包含:class Pip_arrangement: def __init__(self,s1,s2,s3,e,r,N) #传入参数 def point_squar(self)#正方形排布 def pos_stard(self)#第一象限范围筛选 def arrangement(self)#全排布 def visualize(possiton,r)#可视化 def test_visualize()排布类型基本思路为,对于总数N,生成第一象限中(含坐标轴)范围为(N,N)的圆心位置。实际上,可以通过小圆与大圆面积近似相等进一步缩短生成范围以大幅度减少复杂度。粗略计算,集合内元素含量可以由目前的N^2简化到N。这里给出正方形排布的生产程序。def point_squar(self): pos = np.zeros([1,2]) for i in range(self.N): for j in range(self.N): pos = np.append(pos,[[self.s1*j,self.s3+self.s2*(i+1)]],axis=0) pos = pos[1:] return pos范围判断这里判断圆心以及圆是否处于半径范围内的方法仍然是遍历。更改生成范围和采用矩阵化操作都能够大幅度的加快计算速度。遍历的思路是:取出坐标,判断条件满足,满足即放入新数组,不满足扩展大圆半径。def pos_stard(self): pos = copy.deepcopy(self.point_squar()) R = self.s1 + self.e count_tot = 0 count_Y = 0 while count_tot < (self.N-2*count_Y)/4+count_Y: count_Y = 0 pos_stard = np.zeros([1, 2]) for p in pos: if p[0]**2 + p[1]**2 <= (R-self.e-self.r)**2: pos_stard = np.append(pos_stard,[p],axis=0) for pp in pos_stard: if pp[0] == 0.: count_Y = count_Y+1 pos_stard = copy.deepcopy(pos_stard[1:]) count_tot = len(pos_stard) R = R + 1 #mm return R,pos_stard,count_tot坐标扩展仍然是遍历,将第一象限的坐标通过对称操作变换到全部象限空间中。需要注意的是,python对数组的操作会影响原数组,因此需要使用deepcopy的方法。def arrangement(self): pos = copy.deepcopy(self.pos_stard()[1]) pos_first_with_axis_y = copy.deepcopy(self.pos_stard()[1]) R = self.pos_stard()[0] pos_second_without_axis_y = np.zeros([1,2]) for ppp in pos_first_with_axis_y: if ppp[0] != 0: ppp[0] = -ppp[0] pos_second_without_axis_y = np.append(pos_second_without_axis_y,[ppp],axis=0) pos_second_without_axis_y = pos_second_without_axis_y[1:] pos_up = np.append(pos,pos_second_without_axis_y,axis=0) ppos = np.append(pos,pos_second_without_axis_y,axis=0) pos_down = pos_up for q in pos_down: q[1] = -q[1] pos = np.append(ppos,pos_down,axis=0) L =len(pos) return R,pos,L可视化可视化需要先使用matplotlib.artist中的Artist函数,可以帮助我们在确定圆心坐标和半径的情况下批量画出圆。def visualize(possiton,r): dr = [] figure, axes = plt.subplots() for xx in possiton: dr.append(plt.Circle(xx, r, fill=False, lw=0.25)) axes.set_aspect(1) for pic in dr: axes.add_artist(pic) Artist.set(axes, xlabel='X-Axis', ylabel='Y-Axis', xlim=(-300, 300), ylim=(-300, 300), title='Arrangement of heat transfer tubes') plt.savefig('test111.png', dpi=1200, bbox_inches='tight') plt.title('Arrangement of heat transfer tubes') plt.show()用法传入需要的变量,通过Pip_arrangement(s1,s2,s3,e,r,N).arrangement()可以得到半径、位置坐标等信息。def test_visualize(): s1 = 3.2 s2 = s1 * np.sqrt(3)/2 s3 = 2 * s1 e = 0.1 r = 1.1 N = 1000 pipe = Pip_arrangement(s1,s2,s3,e,r,N) pos = pipe.arrangement()[1] visualize(pos,r)全部代码import numpy as np import matplotlib.pyplot as plt from matplotlib.artist import Artist import copy import time class Pip_arrangement: def __init__(self,s1,s2,s3,e,r,N): self.s1 = s1 self.s2 = s2 self.s3 = s3 self.e = e self.r = r self.N = N def point_squar(self): pos = np.zeros([1,2]) for i in range(self.N): for j in range(self.N): pos = np.append(pos,[[self.s1*j,self.s3+self.s2*(i+1)]],axis=0) pos = pos[1:] return pos def pos_stard(self): pos = copy.deepcopy(self.point_squar()) R = self.s1 + self.e count_tot = 0 count_Y = 0 while count_tot < (self.N-2*count_Y)/4+count_Y: count_Y = 0 pos_stard = np.zeros([1, 2]) for p in pos: if p[0]**2 + p[1]**2 <= (R-self.e-self.r)**2: pos_stard = np.append(pos_stard,[p],axis=0) for pp in pos_stard: if pp[0] == 0.: count_Y = count_Y+1 pos_stard = copy.deepcopy(pos_stard[1:]) count_tot = len(pos_stard) R = R + 1 #mm return R,pos_stard,count_tot def arrangement(self): pos = copy.deepcopy(self.pos_stard()[1]) pos_first_with_axis_y = copy.deepcopy(self.pos_stard()[1]) R = self.pos_stard()[0] pos_second_without_axis_y = np.zeros([1,2]) for ppp in pos_first_with_axis_y: if ppp[0] != 0: ppp[0] = -ppp[0] pos_second_without_axis_y = np.append(pos_second_without_axis_y,[ppp],axis=0) pos_second_without_axis_y = pos_second_without_axis_y[1:] pos_up = np.append(pos,pos_second_without_axis_y,axis=0) ppos = np.append(pos,pos_second_without_axis_y,axis=0) pos_down = pos_up for q in pos_down: q[1] = -q[1] pos = np.append(ppos,pos_down,axis=0) L =len(pos) return R,pos,L def visualize(possiton,r): dr = [] figure, axes = plt.subplots() for xx in possiton: dr.append(plt.Circle(xx, r, fill=False, lw=0.25)) axes.set_aspect(1) for pic in dr: axes.add_artist(pic) Artist.set(axes, xlabel='X-Axis', ylabel='Y-Axis', xlim=(-3000, 3000), ylim=(-3000, 3000), title='Arrangement of heat transfer tubes') plt.savefig('test111.png', dpi=1200, bbox_inches='tight') plt.title('Arrangement of heat transfer tubes') plt.show() def test_visualize(): s1 = 3.2 s2 = s1 * np.sqrt(3)/2 s3 = 2 * s1 e = 0.1 r = 1.1 N = 1000 pipe = Pip_arrangement(s1,s2,s3,e,r,N) pos = pipe.arrangement()[1] visualize(pos,r) if __name__ == '__main__': st = time.time() test_visualize() stt = time.time() print(stt-st)运行结果在正方形排布下(六边形懒得做了,优化后会做的),数据来源来自于核动力设备课程大作业——直立式蒸汽发生器中相关参数,1000根管子下的排布,仅仅是1000根,就用时1620s,27分钟!!!!不过得出的结果还算令人满意优劣分析及展望更多的数学准备以减少数据量。对于总数N,生成第一象限中(含坐标轴)范围为(N,N)的圆心位置。实际上,可以通过小圆与大圆面积近似相等进一步缩短生成范围以大幅度减少复杂度。这一步已经算出来了。重复利用矩阵运算的优势。 以Numpy为代表的一系列优秀计算库优化了矩阵运算,大幅度的提高运算速度。相比于遍历的土方法,显然矩阵运算更为优秀。更优的算法。算法灵感来源于蒙特卡洛(特指扔硬币算圆周率那个)(可能因为都有圆),肯定存在更优秀的算法。灵活度。实际存在更严苛的限制条件,可以进一步的拓展可拓展性。算是本篇唯一一个优点了罢,正六边形排布改一下生成就可以实现。总结假期拖延症严重。明天又要线上了。
换热器排管助手V0.9:极低运行效率下的换热器排管及绘制 项目源起大三下学期,涉及了两个关于换热器的课程设计&核动力设备大作业,不出意外,过段时间的课设三也是直立式蒸汽发生器。无论在课设还是大作业,排管始终是一个令人头疼的问题。课设中1.1倍根号下总管数确定中心管数属实令人费解(考虑优化的时候知道是怎么回事了)。核动力设备大作业中也因为没有合理的排布(类圆形)而被老师批评。对于数百个乃至数千根管,如何快速、简便、合理的绘制成了萦绕在我心头解不开的问题。于是从暑假拖到了现在。程序目标程序将要实现:对于给定的管间距参数,在任意排管方式(正方形、正三角形)下,对于任意的管数N,都能够给出一种排布方式及其排布图。且能够被其它程序方便引用。设计思路由于编者能力水平低下,此篇文章中,将介绍一种目前效率极其低下但容易实现的思路。依据排布要求,对于总数N,生成第一象限中(含坐标轴)范围为(N,N)的圆心位置。假定一个半径为R的圆,遍历所有圆心位置,取出所有在圆内且满足边界条件的圆心位置。计算R下符合条件的圆心位置数量是否近似满足总管数在第一象限分布的数量。若不满足,则令R递增,直至满足为止。坐标变换,通过第一象限的点生产全象限的完整分布绘制排布图。思路非常暴力,非常简单,非常低效。但是正在优化,有了初步思路。程序设计总览为了便于调用,整个排布图将设计为类形式,它包含:class Pip_arrangement: def __init__(self,s1,s2,s3,e,r,N) #传入参数 def point_squar(self)#正方形排布 def pos_stard(self)#第一象限范围筛选 def arrangement(self)#全排布 def visualize(possiton,r)#可视化 def test_visualize()排布类型基本思路为,对于总数N,生成第一象限中(含坐标轴)范围为(N,N)的圆心位置。实际上,可以通过小圆与大圆面积近似相等进一步缩短生成范围以大幅度减少复杂度。粗略计算,集合内元素含量可以由目前的N^2简化到N。这里给出正方形排布的生产程序。def point_squar(self): pos = np.zeros([1,2]) for i in range(self.N): for j in range(self.N): pos = np.append(pos,[[self.s1*j,self.s3+self.s2*(i+1)]],axis=0) pos = pos[1:] return pos范围判断这里判断圆心以及圆是否处于半径范围内的方法仍然是遍历。更改生成范围和采用矩阵化操作都能够大幅度的加快计算速度。遍历的思路是:取出坐标,判断条件满足,满足即放入新数组,不满足扩展大圆半径。def pos_stard(self): pos = copy.deepcopy(self.point_squar()) R = self.s1 + self.e count_tot = 0 count_Y = 0 while count_tot < (self.N-2*count_Y)/4+count_Y: count_Y = 0 pos_stard = np.zeros([1, 2]) for p in pos: if p[0]**2 + p[1]**2 <= (R-self.e-self.r)**2: pos_stard = np.append(pos_stard,[p],axis=0) for pp in pos_stard: if pp[0] == 0.: count_Y = count_Y+1 pos_stard = copy.deepcopy(pos_stard[1:]) count_tot = len(pos_stard) R = R + 1 #mm return R,pos_stard,count_tot坐标扩展仍然是遍历,将第一象限的坐标通过对称操作变换到全部象限空间中。需要注意的是,python对数组的操作会影响原数组,因此需要使用deepcopy的方法。def arrangement(self): pos = copy.deepcopy(self.pos_stard()[1]) pos_first_with_axis_y = copy.deepcopy(self.pos_stard()[1]) R = self.pos_stard()[0] pos_second_without_axis_y = np.zeros([1,2]) for ppp in pos_first_with_axis_y: if ppp[0] != 0: ppp[0] = -ppp[0] pos_second_without_axis_y = np.append(pos_second_without_axis_y,[ppp],axis=0) pos_second_without_axis_y = pos_second_without_axis_y[1:] pos_up = np.append(pos,pos_second_without_axis_y,axis=0) ppos = np.append(pos,pos_second_without_axis_y,axis=0) pos_down = pos_up for q in pos_down: q[1] = -q[1] pos = np.append(ppos,pos_down,axis=0) L =len(pos) return R,pos,L可视化可视化需要先使用matplotlib.artist中的Artist函数,可以帮助我们在确定圆心坐标和半径的情况下批量画出圆。def visualize(possiton,r): dr = [] figure, axes = plt.subplots() for xx in possiton: dr.append(plt.Circle(xx, r, fill=False, lw=0.25)) axes.set_aspect(1) for pic in dr: axes.add_artist(pic) Artist.set(axes, xlabel='X-Axis', ylabel='Y-Axis', xlim=(-300, 300), ylim=(-300, 300), title='Arrangement of heat transfer tubes') plt.savefig('test111.png', dpi=1200, bbox_inches='tight') plt.title('Arrangement of heat transfer tubes') plt.show()用法传入需要的变量,通过Pip_arrangement(s1,s2,s3,e,r,N).arrangement()可以得到半径、位置坐标等信息。def test_visualize(): s1 = 3.2 s2 = s1 * np.sqrt(3)/2 s3 = 2 * s1 e = 0.1 r = 1.1 N = 1000 pipe = Pip_arrangement(s1,s2,s3,e,r,N) pos = pipe.arrangement()[1] visualize(pos,r)全部代码import numpy as np import matplotlib.pyplot as plt from matplotlib.artist import Artist import copy import time class Pip_arrangement: def __init__(self,s1,s2,s3,e,r,N): self.s1 = s1 self.s2 = s2 self.s3 = s3 self.e = e self.r = r self.N = N def point_squar(self): pos = np.zeros([1,2]) for i in range(self.N): for j in range(self.N): pos = np.append(pos,[[self.s1*j,self.s3+self.s2*(i+1)]],axis=0) pos = pos[1:] return pos def pos_stard(self): pos = copy.deepcopy(self.point_squar()) R = self.s1 + self.e count_tot = 0 count_Y = 0 while count_tot < (self.N-2*count_Y)/4+count_Y: count_Y = 0 pos_stard = np.zeros([1, 2]) for p in pos: if p[0]**2 + p[1]**2 <= (R-self.e-self.r)**2: pos_stard = np.append(pos_stard,[p],axis=0) for pp in pos_stard: if pp[0] == 0.: count_Y = count_Y+1 pos_stard = copy.deepcopy(pos_stard[1:]) count_tot = len(pos_stard) R = R + 1 #mm return R,pos_stard,count_tot def arrangement(self): pos = copy.deepcopy(self.pos_stard()[1]) pos_first_with_axis_y = copy.deepcopy(self.pos_stard()[1]) R = self.pos_stard()[0] pos_second_without_axis_y = np.zeros([1,2]) for ppp in pos_first_with_axis_y: if ppp[0] != 0: ppp[0] = -ppp[0] pos_second_without_axis_y = np.append(pos_second_without_axis_y,[ppp],axis=0) pos_second_without_axis_y = pos_second_without_axis_y[1:] pos_up = np.append(pos,pos_second_without_axis_y,axis=0) ppos = np.append(pos,pos_second_without_axis_y,axis=0) pos_down = pos_up for q in pos_down: q[1] = -q[1] pos = np.append(ppos,pos_down,axis=0) L =len(pos) return R,pos,L def visualize(possiton,r): dr = [] figure, axes = plt.subplots() for xx in possiton: dr.append(plt.Circle(xx, r, fill=False, lw=0.25)) axes.set_aspect(1) for pic in dr: axes.add_artist(pic) Artist.set(axes, xlabel='X-Axis', ylabel='Y-Axis', xlim=(-3000, 3000), ylim=(-3000, 3000), title='Arrangement of heat transfer tubes') plt.savefig('test111.png', dpi=1200, bbox_inches='tight') plt.title('Arrangement of heat transfer tubes') plt.show() def test_visualize(): s1 = 3.2 s2 = s1 * np.sqrt(3)/2 s3 = 2 * s1 e = 0.1 r = 1.1 N = 1000 pipe = Pip_arrangement(s1,s2,s3,e,r,N) pos = pipe.arrangement()[1] visualize(pos,r) if __name__ == '__main__': st = time.time() test_visualize() stt = time.time() print(stt-st)运行结果在正方形排布下(六边形懒得做了,优化后会做的),数据来源来自于核动力设备课程大作业——直立式蒸汽发生器中相关参数,1000根管子下的排布,仅仅是1000根,就用时1620s,27分钟!!!!不过得出的结果还算令人满意优劣分析及展望更多的数学准备以减少数据量。对于总数N,生成第一象限中(含坐标轴)范围为(N,N)的圆心位置。实际上,可以通过小圆与大圆面积近似相等进一步缩短生成范围以大幅度减少复杂度。这一步已经算出来了。重复利用矩阵运算的优势。 以Numpy为代表的一系列优秀计算库优化了矩阵运算,大幅度的提高运算速度。相比于遍历的土方法,显然矩阵运算更为优秀。更优的算法。算法灵感来源于蒙特卡洛(特指扔硬币算圆周率那个)(可能因为都有圆),肯定存在更优秀的算法。灵活度。实际存在更严苛的限制条件,可以进一步的拓展可拓展性。算是本篇唯一一个优点了罢,正六边形排布改一下生成就可以实现。总结假期拖延症严重。明天又要线上了。