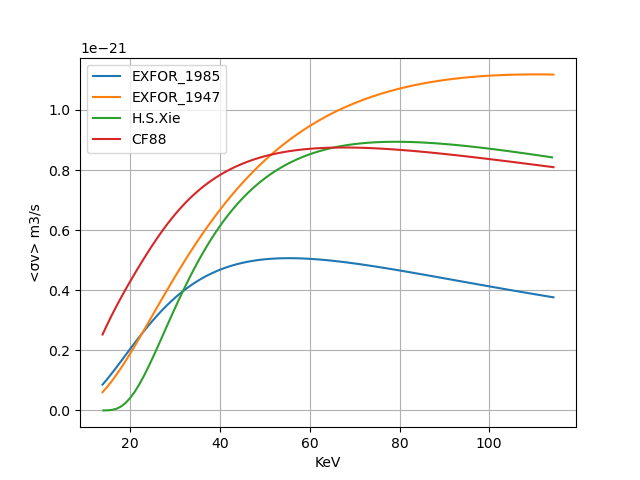
磁约束聚变原理与装置之一——重元素聚变可行性 相关代码上传至MCFCourse/HeavyFusion at main · DMCXE/MCFCourse (github.com)1. 请列出《流浪地球》地球发动机中可能会发生的聚变反应1.1 背景”重元素聚变是一门很深的学问...比如我们所在的华北794号，全功率运行时能对大地产生一百五十亿吨的推力[1]“地球发动机作为《流浪地球》系列中最具有吸引力的科幻概念之一，其基于重元素聚变设想最初来源于刘慈欣所著短篇小说《流浪地球》，并完善于郭帆导演电影《流浪地球2》中。根据上述设定，地球发动机所依赖的重元素聚变技术通过燃烧石头——即硅元素聚变，产生大量能量。例如反应1428Si+1428Si→2856Ni+γ+E在现实宇宙，硅元素聚变过程发生在质量至少为8-11个太阳质量的大质量恒星中，这一过程一般由 $\alpha$​ 过程驱动，即硅元素不断与氦核结合直到生成镍乃至之后的元素。在该反应成立的前提下，需要提供大量的能量加热这一过程，因此在《流浪地球2》设定中，需要通过灌有氦-3燃料的迷你氢弹——”火石“完成初始点火。此外，《流浪地球》系列具有一条相对完整的重元素聚变技术发展时间线：2002.03 以色列科学家Yaffa Radclyffe 开始研究可控核聚变—— 2016.06 Yaffa Radclyffe在可控核聚变实验中意外去世——2018.09 Yaffa Radclyffe的学生中田一夫在老师最后一次失败结果中发现重聚变现象——2025 中田一夫成功制作第一台重聚变航天发动机。鉴于现实宇宙中2024年ITER仍然遥遥无期，对于轻核可控核聚变点火仍属于部分科学幻想。[1] 朔方等，流浪地球2电影制作手记. 北京:中信出版社. ISBN 978-7-5217-4972-41.2 现实宇宙中可能发生的重聚变反应地壳中氧元素占地壳化学成分总量约48.6%，硅元素占地壳化学成分总量约26.3%，两者的化合物二氧化硅广泛的存在与岩石中，因此，对于烧石头的地球发动机，将主要的聚变反应锁定在氧燃烧与硅燃烧过程。氧燃烧过程的主要反应(生成元素非同位素)：  816O+  816O→1428Si+24He+9.593MeV如果考虑全部可能的反应，则写为:816O+816O→1428Si+24He+9.593MeV→1531P+11H+7.676MeV→1631 S+n+1.459MeV→1430Si+211H+0.381MeV→1530P+12D−2.409MeV硅燃烧过程设计的反应较为繁琐，在天体中，硅聚变为镍的过程1428Si+1428Si→2856Ni+γ+E是由数个被称为 α​过程 的反应组成的，即从硅开始每次结合一个氦核生成重元素、并持续至镍及其之后的元素1428Si   +24He −>1632S     +γ ,E=6.95 MeV1632S    +24He −>1836Ar   +γ ,E=6.64 MeV1836Ar  +24He −>2040Ca  +γ ,E=7.04 MeV2040Ca +24He −>2244Ti   +γ ,E=5.13 MeV2244Ti  +24He −>2448Cr  +γ ,E=7.70 MeV2448Cr +24He −>2652Fe   +γ ,E=7.94 MeV2652Fe +24He −>2856Ni   +γ ,E=8.00 MeV在恒星中， α过程在镍附近由于与photodisintegration效应相互作用导致平衡以结束。因此，对于实现重元素聚变的考虑将侧重于对氧燃烧与硅燃烧，并尝试将硅燃烧中的 α过程 整合为硅直接聚变过程。2. 在这写可能的聚变反应中，哪一种最有可能是驱动地球发动机的主要反应？可以通过分析上述反应截面或反应速率以分析上述反应的可行性。相关截面或反应速率数据将主要取自已有的数据库。2.1 聚变反应数据库2.1.1 CF88简介Thermonuclear Reaction Rates V，Georgeanne R. Caughlan and William A. Fowler，Aomic Data and Nuclear Data Tables ，Volume 40, #2, p. 283-334热核反应速率 --- Thermonuclear Reaction Rates (csdb.cn)Caughlan and Fowler 1988 Thermonuclear Reaction Rates 数据库，简称CF88数据库，数据集来自 Georgeanne R. Caughlan 与 William A. Fowler 收集整理自1987年8月之前的实验信息，提供了氢至硅的核天体物理学中的重要热核反应速率，给出了其反应速率的拟合表达式。2.1.2 EXFOR简介N. Otuka et.al Towards a More Complete and Accurate Experimental Nuclear Reaction Data Library (EXFOR): International Collaboration Between Nuclear Reaction Data Centres (NRDC),Nuclear Data Sheets,Volume 120,2014, Pages 272-276, ISSN 0090-3752, https://doi.org/10.1016/j.nds.2014.07.065.EXFOR：实验核反应数据 --- EXFOR: Experimental Nuclear Reaction Data (iaea.org)Experimental Nuclear Reaction Data 数据库，简称EXFOR数据库，至今已包含24915个与中子、带电粒子、光子相关核反应的实验数据，根据实验数据来源分为若干属性，与热核反应相关数据大部分采用储存反应截面。2.1.3 数据格式与换算CF88中储存了目标反应的反应Q值(MeV)与反应速率 f(cm^3/moles/s) ，拟合区间为 10^6-10^10K，用 T9 (10^9)表达。在计算点火时可以通过单位换算后直接使用。EXFOR中储存了多种面向核物理从业人员的数据，对于关心的反应截面数据，保存为b或mb，能量为KeV或MeV，在数据文件中会特别说明。为了与CF88比较以及执行之后的点火计算，需要将其计算为聚变反应率 <σv> (m^3/s)。一般的聚变反应率定义为<σv>=∫∫dv1dv2σ(|v1−v2|)|v1−v2|f1(v1)f2(v2)其中 f1,f2 表示为两种离子的归一化分布函数。当两种离子都采用麦克斯韦分布时，反应率写为<σv>M=8πmr1(kBTr)3/2∫0∞σ(E)exp⁡(−EkBTr)dE其中，mr = m1m2 / m1+m2表示为有效质量，Tr = m1T1+m2T2/m1+m2​表示为有效温度。对于离散数据可直接通过离散积分计算、或在满足物理特征的拟合多项式下进行计算。不难发现，在数据边界处精度将下降。2.1.4 数据丰富性重元素聚变常见于大质量天体中，能否在实验室环境实验并采集数据是验证后续重元素聚变可行性的重要基础之一。换言之，关心数据库中的反应数据能量范围是否足够广、是否包含了需要的数据。在前述聚变反应中，能在数据集中获取的反应为：  816O+  816O→1428Si+24He1428Si+24He→1632S  816O+  816O→Fusion1428Si+1428Si→Fusion即我们无法按照设想的去分析全部的 $\alpha$过程。对于上述反应式的后两个，描述了关于氧16与硅28的全部聚变反应总实验截面，因此需要在后续工作中选择合适的聚变反应能量以进一步讨论。2.2 不同数据库间及数值方法的验证进行聚变的可行性分析前，首先需要验证CF88与EXFOR数据的准确性、采用数值方法的正确性，以此为前提才能够保证后续的比较是可信的。氘氚反应：D+T→n+24He是目前科技阶段适合人类采用的聚变反应之一，有大量的对于该聚变截面的分析。将通过对照CF88、EXFOR与H.S.Xie[1]书中的DT反应率曲线以验证数据库的可用性。在上述三个比较源中，EXFOR由于采用实验数据，因此数据能量范围较为窄，在以EXFOR为基准能量范围下，可得聚变反应率如下图所示注意到，H.S.Xie数据与CF88数据在峰值量级与趋势上较为一致，而EXFOR的两个数据集均有或高或低的数值误差，并展现了强烈的数据集依赖性。因此通过比较EXFOR中两个数据的趋势与量级可以排除数值方法引入大误差，并将后续比较范围拓宽至量级的一致性上。另外，需要进行该项验证的另一个原因是，CF88库中的能量上限为 $10^{10}J\sim 861.73KeV$​，而实际上重元素聚变的苛刻条件难以在该区间中找到理想的解，为此需要依赖EXFOR的高能实验数据进行拓展以尝试找到可以接受的参数区间。[1] 谢华生. 聚变点火原理概述.2023.安徽:中国科学技术大学出版社.ISBN 97873120567342.3 重元素聚变速率比较2.3.1 O16(O16,A)Si28在2.1.4中表述了可用的聚变反应数据。对于氧燃烧生成硅28的过程，来自CF88与EXFOR的反应速率为：对于CF88的数据范围，即不超过1MeV的能量中，最大能达到的反应速率不超过 2x10^-26m^3/s，在EXFOR的三组数据中，最大约能在35MeV能量下达到 5.6x10^-23m^3/s的反应速率。2.3.2 O16(O16,)FUS如果不考虑某一具体的反应道而关系全部的聚变反应，氧燃烧的聚变反应率为数据库中的三个反应的反应率均处于10{-22m^3/s, 高于O16(O16,A)Si28反应一个量级（或在10MeV-30MeV区间内达到相同量级），在约15MeV时取得最大聚变反应率。2.3.3 Si28(Si28,)FUS如果不考虑某一具体的反应道而关系全部的聚变反应，硅燃烧的聚变反应率为数据库中的三个反应的反应率均处于10^{-22}m^3/s, 在约35MeV时取得最大聚变反应率。反应率的量级与O16(O16,)FUS一致。但是很难解释为什么D0750002与E1435016在相同的能量下反应速率相差7倍，可能的解释是实验环境导致了不同的聚变反应道组合。2.3.4 对比考虑将 O16(O16,)FUS与Si28(Si28,)FUS进行对比，如下图所示尽管氧燃烧与硅燃烧处于相同的量级，但氧燃烧达到速率峰值所需要的能量只有硅燃烧的一半。2.4 重元素聚变功率比较2.3.3与2.3.4中的实验只测得了发生聚变反应的截面，但无法确定发生了那种反应，释放了多少能量。这里进行一个大胆的假设。对于氧燃烧，结合2.3.1与2.3.3的反应速率差距，假设释放的主要能量来源于生成Si28的反应，部分来自于生成P31的反应，释放总能量为9.593+7.676/2=13.431 MeV; 对于硅燃烧，其蕴含的α过程释放的总能量为49.4MeV，假设其每个过程释放的能量占比减半，则释放总能量约为13.525625MeV。聚变功率表达为：单位体积聚变功率Pfus为反应次数乘以单次反应释放的能量Y：Pfus=11+δ12n1n2<σv>Y聚变功率与反应率是线性关系。因此在硅氧燃烧反应相近的前提下，单次反应释放的能量越多，则聚变功率越大。2.5 结论如前所述，我们尚且无法准确衡量那个反应道参与了主要的反应。因此在第二章讨论末尾，给出定性回答：尽管氧燃烧峰值截面所需能量低于硅燃烧，但硅燃烧产生的能量范围远超氧燃烧，从能量角度，硅燃烧是适合作为最终聚变能源的主要燃料。3.评估重元素聚变反应的理想点火条件3.1 理想点火条件理想点火条件即被约束的聚变等离子体满足聚变产生的带点产物能量能够沉积到等离子体中。在仅考虑轫致辐射时，理想点火条件为聚变产物中带电部分功率大于韧致辐射功率时的温度。在弱相对论下，轫致辐射表达为Pbrem=CBne2kBTe{Zeff[1+0.7936kBTemec2+1.874(kBTemec2)2]+32kBTemec2}[W⋅m−3]其中，$Z_{eff}$ 表示为有效电荷数，当反应物相同时等价为离子电荷数。与2.4中的聚变功率曲线相对比寻找相交点，即可获得是否满足理想点火条件的条件。由于CF88数据库中能量区间远远小于其它截面数据，因此舍弃，则全部聚变功率与韧致辐射功率在 ne = 1x10^21 m^-3下为:（注意纵轴为功率，标识符打错）选定截面在区间内的聚变功率无法与轫致辐射功率相交，因而不存在点火点。3.2 能量增益因子定义能量增益因子Q：Q=Pout−PinPin当满足点火条件时，即聚变体系能够稳态运行并且无需外加功率，对应Q → ∞。现在考虑是否能够实现有限的Q，例如Q=1的能量得失相当。考虑增益因子与轫致辐射的劳森判据可以写为：neτE=32kB(Te+Ti/Z)(1/Q+fion)1+δ12x1x2Zi2<σv>Y−CBkBTeZeffgeff这里的 geff为轫致辐射中的geff=[1+0.7936kBTemec2+1.874(kBTemec2)2]+1Zeff32kBTemec2计算Q=1时的点火数据（能量拓宽后）即对于上述各类反应在10MeV能量附近，能够达到较低的密度约束时间乘积，约为 10^24 m^-3s。对于目前典型聚变堆的密度 10^21 m^-3,则要求能量约束时间为1000s。一般而言，天体中发生的核反应往往不需要达到点火温度即可进行，这样可以解释为什么点火不可行而一定Q值的可行。3.3 结论基于已有实验数据，在麦克斯韦分布下，考虑轫致辐射时，无法实现氧或硅的自持燃烧过程。但仍然有希望实现有限Q的能量得失相当。同样由3.1不难发现，能量最高的反应为硅系列的燃烧，考虑氧燃烧与硅燃烧在Q=1时所需要的能量相近，因此硅燃烧是驱动发动机的主要反应。一方面足以提供大量能量，另一方面硅燃烧过程与Fe的最终形成息息相关，铁可以作为地球发动机产生巨大推力的工质。此外，无需担心初始的能量过高，在设定中，需要”火石“——即氦-3为燃料的氢弹进行点火，能够满足初始的能量需求。4. 讨论可以改变哪些条件使得这种“重元素聚变”更加可行4.1 非麦克斯韦分布热化粒子分布在上述计算时，通过截面计算反应率采用的是麦克斯韦分布，而引发聚变的只要粒子聚集在分布的高能尾上，而麦克斯韦分布对应的这部分占比非常小。如果能够将粒子分布从麦克斯韦分布转为高能。参照[xie 2022]中的截面公式：<σv>=2πmrkB2TrTd∫0∞σ(E)Eexp⁡(−E+EdkBTr)sinh⁡(2EEdkBTr)dE当注入10MEV粒子束后，发现氧燃烧输出功率（注意纵轴为功率，标识符打错）如下图所示：氧燃烧开始和韧致辐射产生交点，尽管存在很大的数值误差，且使得整体产生10MeV的相对漂移速度不现实，但是能够实现理想点火条件。4.2 $\mu$子催化聚变Muon-catalyzed fusion，由于μ子具有与电子相似的性质，能够与原子核结合屏蔽库伦部分库伦势以提升反应率。但是，μ子对聚变产物He4有更高的结合截面，因此在DT、DD聚变中难以在μ子与聚变产物He4结合前以及衰变前反应足够多的次数。但是在可能发生的硅燃烧过程中，由于硅燃烧反应大概率依赖 α过程，而潜在的μ子与α粒子结合能够提高α过程的反应截面。关于μ子参与的α过程，这只是个人的科学幻想，有待理论或实验验证。4.3 精细化截面数据由于现存的热核聚变反应实验数据库中囊括的截面数据教少、能级较为分散，可能存在错过部分共振峰的情况。如果精细化截面数据，也许能够提升整体聚变反应率。