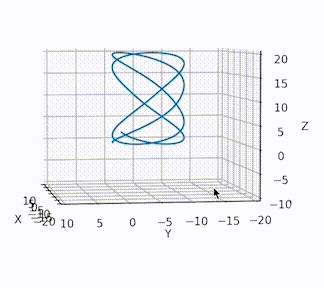
单粒子在场中的运动（一）：一种粗糙的计算 项目源起在亚布力的时候，偶然的一次滑水，在GitHub上找到了某个描述在某个感兴趣装置中的粒子运动模拟。欣喜之余仔细阅读了源码与作者的项目介绍，不免大失所望，不仅缺乏很多必要的头文件，且作者直言并没有足够的知识去解决这个问题。因此处于好奇，不免想要尝试一下。（虽然经过短暂的构思，发现确实存在很多问题）。初期尝试由于先前想要计算的问题十分复杂，而且发生的过程极快，因此难以在现有知识水平下进行程序的搭建。突然想到了某些圣遗物和某个被封了很多年知识科普团队，于是定下了第一步计划：在不考虑粒子间相互作用、不考虑相对论效应、不考虑Maxwell方程的前提下，单粒子或多粒子在常电磁场中的三维运动可视化。且求解过程基于物理方程描述。（即忘记粒子是如何在场中运动的结论）目录{timeline}{timeline-item color="#19be6b"}物理过程的数学表达{/timeline-item}{timeline-item color="#19be6b"}程序化准备{/timeline-item}{timeline-item color="#19be6b"}Codeing{/timeline-item}{timeline-item color="#19be6b"}运行结果{/timeline-item}{timeline-item color="#ed4014"}缺点分析及展望{/timeline-item}{timeline-item color="#ed4014"}结束语{/timeline-item}{/timeline}物理过程的数学表达“当听者以为自己已有所得时，真正的内行会觉得连皮毛也不是。” ――克莱因，《数学在19 世纪的发展》 我想，单粒子轨道这个看似简单的问题可能也深邃到我们尚只理解其皮毛 。 ——《计算等离子体物理导论》单粒子在场中运动，从入门角度而言，任何上过高中的理科生都可以回答这个问题：磁场改变运动方向，电场改变粒子速度。通过高中的大量训练，我们知道如何联立洛伦兹力与向心力求解平面中的粒子运动，复杂一点的情况下，小球受轨道电场力平抛等等。再最开始，我也想直接进行一番物理计算，把运动模式给出来，即给出闭式方程。但这显然是不科学的。场在空间的复杂分布会超出我们的计算能力，且并不是所有物理过程的数学描述都有通解。在电磁场中，带电粒子所受的洛伦兹力为：运动轨迹由Newton‘s Law给出：通过以上方程组，理论上可以求解出空间中粒子在常电磁场作用下的任意运动。程序化准备接下来我们简要的分析一下，为程序化做准备（离散化方程）。在笛卡尔坐标下，任何物理量都可以由三维分量表示，比如：电场E = [E_x,E_y,E_z]，磁场B =[B_x,B_y,B_z]，场力F = [F_x,F_y,F_z]粒子速度V= [v_x,v_y,v_z]，粒子位置Position= [X,Y,Z]对于任意时刻t，都可以计算出时刻t下的F，由：采用向后差分（方程的解可由初始条件确定），可离散化为：整理为：得到当前时刻下的速度，进一步可以得到当前时刻的位置，由整理为：最后，我们能够得到代求解的方程组为：当然，用前朝的剑斩本朝的官，肯定存在大问题。后文会总结，未来会改进。在程序（Python）中，这段表示为：F = p.q * (E + np.cross(p.v,B)) p.v = p.v + F * (timestep/p.m) p.pos = p.pos + p.v * timestep如果采用比如数学功能较强的软件，只需要给出最开始的数学描述微分方程即可。Codeing剩下的工作就是Coding，让它能够在符合语法规范的情况下运行。总的来看，主要包含以下几个模块：class Particle #粒子 class Field #场 class ParticleSimulator #粒子运动 def visualize(simulator) #可视化 def test_visualize() #运行粒子粒子是粒子仿真的重点，具有质量与电荷，需要定义初始位置与初始速度。定义粒子类：class Particle: def __init__(self,start_pos,v,mass,Quantity): #start_pos , v is 3 dim self.pos = start_pos self.m = mass self.q = Quantity self.v = v self.sum = np.zeros([1,3]) #储存粒子的历史位置场场是粒子在场中运动的重点，目前虽然是单一指向的常场，但长远考虑，需要建立一个场类：class Field: def __init__(self): ''' self.B = np.array([20, 20, 30]) self.E = np.array([10., 20.,-15]) ''' self.B = np.array([0, 0, 0.5]) self.E = np.array([0, 0, 0.2])粒子仿真粒子仿真按时步进行，对于每一个时步求解上述方程组并更新粒子位置与记录路径总和。在一个ParticleSimulator类中，对于时间dt的更新方式为：def evolve(self,dt): #参数传入更新时间dt timestep = 1e-3 #确定更新的最小时步 nsteps = int(dt / timestep) #分割时间内计算空间 #传入场参数 f = self.f B = f.B E = f.E for i in range(nsteps): for p in self.particles: #控制方程求解 F = p.q * (E + np.cross(p.v,B)) p.v = p.v + F * (timestep/p.m) p.pos = p.pos + p.v * timestep p.sum = np.append(p.sum,[p.pos],axis=0)可视化可视化利用matplotlib库中的animation.FuncAnimation()函数，对于指定的ParticleSimulator.evolve粒子运动更新方式，按照函数传入的设定参数进行绘制更新。这里更多的是函数的使用方式。比如绘制时.set_data()方法只允许传入两个坐标参数，第三维需要额外使用.set_3d_properties()传入。更多的细节不再赘述。line.set_data(X[i],Y[i]) line.set_3d_properties(Z[i])使用方式在一个定义的test_visualize()中，首先设定粒子信息：#单粒子时 particles = [Particle(position, v, mass, q)] #多粒子时 particles = [Particle(position1, v1, mass1, q1), Particle(position2, v2, mass2, q2), Particle(position3, v3, mass3, q3)]接着设定场field = Field()传入仿真参数simulator = ParticleSimulator(particles,field)可视化visualize(simulator)运行时调用test_visualize()即可。代码总览import numpy as np import matplotlib.pyplot as plt import matplotlib.animation as animation class Particle: def __init__(self,start_pos,v,mass,Quantity): #start_pos , v is 3 dim self.pos = start_pos self.m = mass self.q = Quantity self.v = v self.sum = np.zeros([1,3]) class Field: def __init__(self): self.B = np.array([0, 0, 0.5]) self.E = np.array([0, 0, 0.]) class ParticleSimulator: def __init__(self,particles,Field): self.particles = particles self.f = Field #最小时间dt内更新轨迹 def evolve(self,dt): timestep = 1e-3 nsteps = int(dt / timestep) f = self.f B = f.B E = f.E for i in range(nsteps): for p in self.particles: F = p.q * (E + np.cross(p.v,B)) p.v = p.v + F * (timestep/p.m) p.pos = p.pos + p.v * timestep p.sum = np.append(p.sum,[p.pos],axis=0) def visualize(simulator): X = [p.pos[0] for p in simulator.particles] Y = [p.pos[1] for p in simulator.particles] Z = [p.pos[2] for p in simulator.particles] fig = plt.figure() ax = fig.add_subplot(projection = "3d") line, = ax.plot(X, Y, Z) ax.set(xlim3d=(-20,10), xlabel='X') ax.set(ylim3d=(-20,10), ylabel='Y') ax.set(zlim3d=(-10,20), zlabel='Z') def init(): line.set_data([], []) line.set_3d_properties([]) return line, def init2(): line.set_data([], []) line.set_3d_properties([]) return line def animate(i): simulator.evolve(0.1) X = [p.sum[:,0] for p in simulator.particles] Y = [p.sum[:,1] for p in simulator.particles] Z = [p.sum[:,2] for p in simulator.particles] line.set_data(X[i],Y[i]) line.set_3d_properties(Z[i]) return line, anim = animation.FuncAnimation(fig, animate, frames=len(X), init_func=init, blit= True, interval=1) plt.show() def test_visualize(): p1 = np.array([0, 0, 0]) v = np.array([1,0,0]) particles = [Particle(p1, v, 3, 1)] field = Field() simulator = ParticleSimulator(particles,field) visualize(simulator) if __name__ == '__main__': test_visualize()运行结果运行环境处理器：基于Apple Silicon的Arm64构架的M1内存：16GB DDR4操作系统：macOS Monterey 12.4语言：miniforge虚拟环境下的Python3.9具有初速度的粒子在恒定磁场下运动带电粒子在具有一定沿X方向初速度，在沿Z方向恒定磁场下运动，所得的图像如下图所示：根据高中知识可以知道，是圆形轨道。具有初速度的粒子在恒定电磁场下运动带电粒子在具有一定沿X方向初速度，在沿Z方向恒定电磁场下运动，所得的图像如下图所示：初速度为0的粒子在任意电磁场下的运动带电粒子在某一任意指向电磁场下的运动如下图所示：单粒子在受控电磁场下被约束理想情况下，单粒子在受控的电磁场作用下被约束在特定范围内。多粒子程序在二维平面内支持多粒子运动，但当拓展至三维空间内，由于程序逻辑，粒子是交替产生的。缺点分析及展望目前，该项目存在非常多的缺陷。计算逻辑低效。本次演示的计算逻辑为绘图驱动计算。即计算过程是伴随着动画的渲染而不断更新的。因此运行低效、处理困难、规模繁琐。——改进方向：先进行粒子运动计算，再由数据驱动路径绘制。数值解法能量耗散。向后差分的方法会造成体系能量的耗散，会造成系统随着时间演化精度不断下降。——改进方向：采用更先进的差分方法，比如通过哈密尔顿量计算，确保体系完备。运行效率低。随着运行时间增长，Particle中存储了大量的解，且每次绘图都需要重新遍历，时间开销逐步增大。通过改进缺点1可以克服物理场复杂化计算可靠性未验证。当物理场随着空间分布后，计算是否任然可靠未验证。拓宽粒子相互作用与Maxwell方程组结束语又是不务正业的几天时间，别人该写实习报告的写实习报告，该学习预习的预习，该搞项目的搞项目；能力不足还想学人造轮子，只能是自讨苦吃！