搜索到
1
篇与
遗传算法
的结果
-
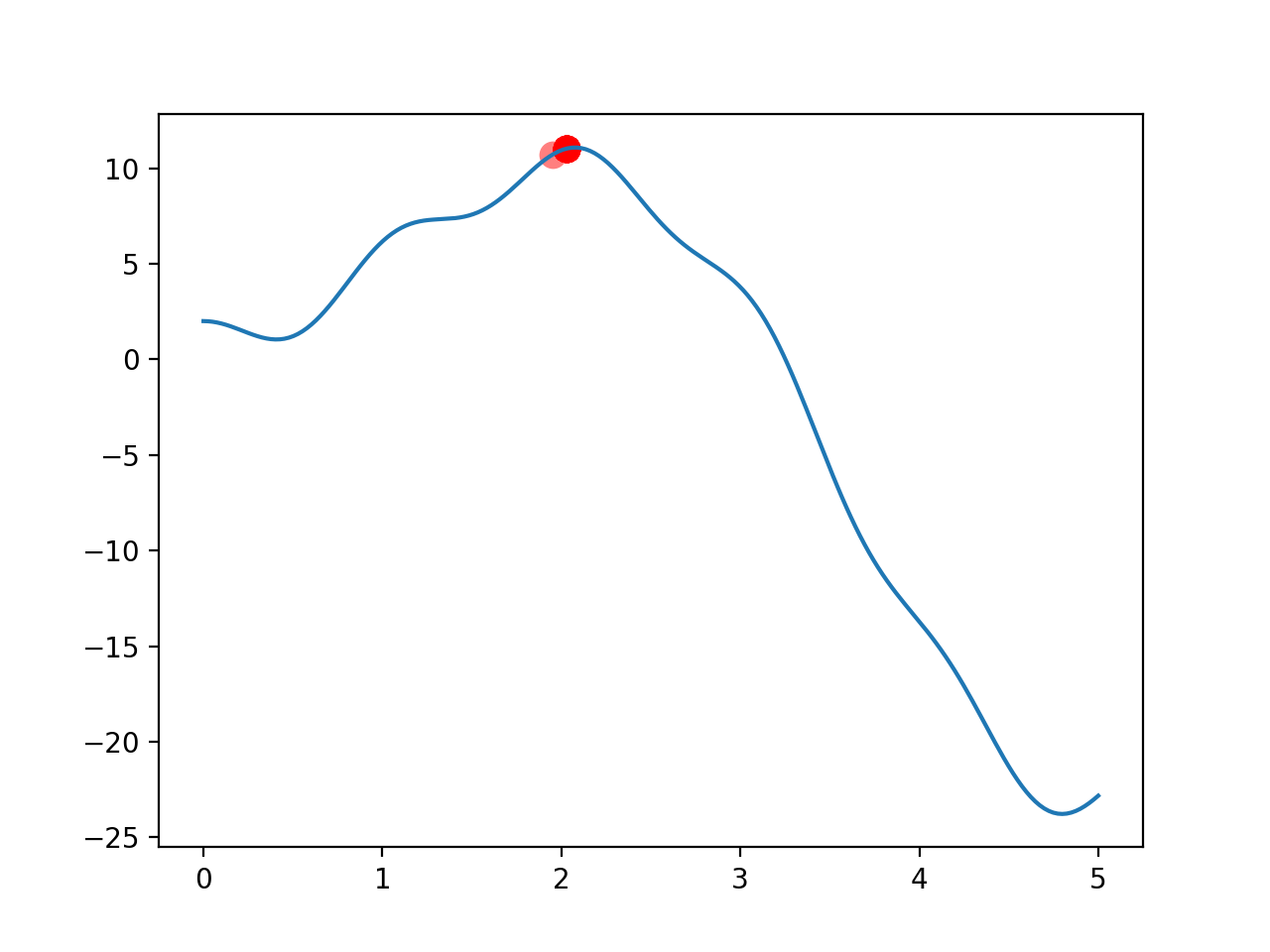
 遗传算法学习笔记一:重新发明简易轮子 想起高中,不妨回忆一下生物必修二在记忆中所占的权重。想一想刷遗传题时的痛苦和折磨,想一想减数分裂的框图有多长,生物老师让你默写过多少次减数分裂框图,最后生物必修二内容又能拿多少分。但这些可以是一个有趣的数学问题。为了让一个实际问题变得更容易贴合生物学实际,咱们先从二维函数极值点问题出发,去初步感受一下轮子是怎么变圆的。摘抄自百度百科:“遗传算法(Genetic Algorithm,GA)最早是由美国的 John holland于20世纪70年代提出,该算法是根据大自然中生物体进化规律而设计提出的。是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。该算法通过数学的方式,利用计算机仿真运算,将问题的求解过程转换成类似生物进化中的染色体基因的交叉、变异等过程。”对于遗传算法,核心有如下几个:1、figness适应度函数2、select选择3、crossover交叉4、mutantion变异这些概念可以十分轻松的在高中生物必修二中发现。这次我们将通过计算机方法去实现这个神奇的过程。因为站在如今人类的知识层级上,遗传算法塑造了我们,还让我们发现了遗传算法。其实我也不太记得人类是不是有丝分裂了,但是减数分裂还是记得的。但无论是何种分裂,核心是生物体的遗传信息存在与DNA中,DNA是携带遗传信息的长链,由四种碱基的不同排列组成了构成了纷繁复杂的生物体,以及他们各自的功能。没有DNA的此种特性,Shakespeare就无法love, write, sigh, pray, sue, and groan。也许DNA是图灵完备的,但是人类已经掌握二进制了,只需要两个数字即可构建如今的数字帝国。因此,进行遗传算法的第一项,就是将待求量二进制化。DNA = np.random.randint(2,size=(DNA_SIZE))此方法可以构建出由0,1组成,长为DNA_SIZE的表征二进制的数组。对于一定数量的种群,对每个种群个体分配DNA序列:#pop(population)为[0,2),popsize个,每个长为dnasize的随机数矩阵 #换言之,即由0,1组成的dna长链,种群中每个个体都不相同。 pop = np.random.randint(2,size=(POP_SIZE, DNA_SIZE)) 对于一个二进制数,它均可对应唯一一个十进制整数。由于用二进制非浮点数表示一个非整数数复杂的。因此我们可以采用一种比例放缩的方法。对于一个八位二进制数,可以对应0-255此256个十进制整数。将此256个数归一化再乘上目标求解区间长度。就可以得到具备一定精确度的取值空间了。这个过程可以看作转译过程,算法为:def translateDNA(pop): return pop.dot(2**np.arange(DNA_SIZE)[::-1])/float(2**DNA_SIZE-1)*X_BOUND[1] 其中,X_BOUND=[0,5]接下来,就可以放心构建算法核心了!对于要求解极大值的函数:def F(x): return np.sin(x)*5*x + np.cos(6*x)+1 构建与之相关的fitness适应函数:def get_figness(Y_values): return Y_values + 1e-5 - np.min(Y_values) # y_i值-所有y构成数组的最小值+定义的无穷小量 #遗传算法中不能出现负数,所以要加上无穷小量这个适应函数表征了某个体与最小适应性个体的差值。由于该问题是极大值问题,因此越大越好。Fitness的值可以表征选择该个体的适应性优劣,并可以在Select选择运算内作为选择个体的概率Select选择:在该环节内,要依据适应性能挑选出较优个体,模拟自然选择过程。将fitness的值传入该模块作为每个个体的选择权重。def select(pop,fitness): #注意random.choice函数:依据概率p在指定数组中选择在指定的数组中随机采样 idx = np.random.choice(np.arange(POP_SIZE),size= POP_SIZE,replace=True, p=fitness/fitness.sum()) return pop[idx] #随机选择种群中都某一个个体,表征个体的是他的dna 选择出来的大概率是适应性高个体,小概率是适应性个体。一时的失败不算是失败,运气也是实力的一部分也许。Crossover交叉环节:实际生物体遗传时,染色体见会发生交叉互换的情况。这里我们简化这种交叉互换,采用随机数的方式随机选择亲本处需要替换的地方。将亲本1的部分序列值由序列2对应部分替换,形成子代。这里用到的算法比较有意思,运用了bool类型在数组中的选择作用。首先我们生产与DNA等长的随机序列,并将其转换为bool类型:cross_points = np.random.randint(0,2,DNA_SIZE).astype(np.bool_) 输出形式为:[ True True False False False False True True False True]对于数组a而言,a[crossover_point]选择了所有bool类型为true的元素;而b[c_p]=a[c_p]就是将a中true的元素赋予b中true元素对应的位置上。进而完成交叉这一行为。def crossover(parent, pop): if np.random.rand()<CROSS_RATE: index = np.random.randint(0,POP_SIZE,size=1) cross_points = np.random.randint(0,2,DNA_SIZE).astype(np.bool_) #corssover的原理是由于cross_point被定义为了布尔类型: #对于数组a而言,a[crossover_point]选择了所有bool类型为true的元素 #b[c_p]=a[c_p]就是将a中true的元素赋予b中true元素对应的位置上。完成交叉。 parent[cross_points]= pop[index, cross_points] return parent mutation 变异:学核科学的,自然知道在辐射条件下基因会发生突变。因此,基因可能会发生良性突变,也可能发生恶性突变,但是总会有几率突变。定义突变机率:MUTATION_RATE = 0.003 def mutation(child): for point in range(DNA_SIZE): if np.random.rand()< MUTATION_RATE: if child[point] == 1: child[point] = 0 else: child[point]=1 return child (注意结合主循环内内容,之后会展示,此时,child已经变成一个体了)到此为止,我们已经得到了构成一个普通遗传算法的几个关键函数。接下来构建主函数,连接起各核心功能;流程图如下,图片抄自百度百科:定义种群生长代数:GENERATIONS=200对于每代种群:1、获取目标函数值:F_value = F(translateDNA(pop))2、获取个体适应度fitness = get_figness(F_value)3、Select选择:依据适应度选择多个个体并填充全部种群pop = select(pop,fitness)创建另一个亲本,采用复制的方式pop_copy=pop.copy()4、对于每一个个体与其另一亲本进行crossover交叉配对,且随之变异for parent in pop: child = crossover(parent,pop_copy) child = mutation(child) parent[:] = child #完整复制一遍,同时更改了pop本身 完整代码如下:import numpy as np import matplotlib.pyplot as plt DNA_SIZE = 20 X_BOUND=[0,5] POP_SIZE = 10 CROSS_RATE= 0.8 MUTATION_RATE = 0.003 GENERATIONS = 200 #GA作用的目标函数 def F(x): return np.sin(x)*5*x + np.cos(6*x)+1 #GA的核心:fitness适应度,评价子代的指标。 def get_figness(Y_values): return Y_values + 1e-5 - np.min(Y_values) # y_i值-所有y构成数组的最小值+定义的无穷小量 #遗传算法中不能出现负数 #在范围内将x编码成二进制数,并且将二进制数缩放到所需要的范围内。 #pop(population)是一个储存二进制DNA的矩阵,形状与POP_SIZE和DNA_SIZE相关。 #pop.dot(2**xxx)的部分实际上是利用数权法进行2-10进制转换;.dot是返回两个向量内积 def translateDNA(pop): return pop.dot(2**np.arange(DNA_SIZE)[::-1])/float(2**DNA_SIZE-1)*X_BOUND[1] ''' 进化的三要素:选择:select;交叉:crossover;变异:mutation ''' #第一步,选择 def select(pop,fitness): #注意random.choice函数:依据概率p在指定数组中选择在指定的数组中随机采样 idx = np.random.choice(np.arange(POP_SIZE),size= POP_SIZE,replace=True, p=fitness/fitness.sum()) return pop[idx] #随机选择种群中某一类个体并替换全部个体,选择后种群内个体几乎是适应性强的,表征个体的是他的dna #第二步,交叉配对 def crossover(parent, pop): if np.random.rand()<CROSS_RATE: index = np.random.randint(0,POP_SIZE,size=1) cross_points = np.random.randint(0,2,DNA_SIZE).astype(np.bool_) #corssover的原理是由于cross_point被定义为了布尔类型: #对于数组a而言,a[crossover_point]选择了所有bool类型为true的元素 #b[c_p]=a[c_p]就是将a中true的元素赋予b中true元素对应的位置上。完成交叉。 parent[cross_points]= pop[index, cross_points] return parent #第三步,变异 #child在主循环里已经定义为pop内的某一个体,因此只需要考虑dna上有多少基因需要突变即可。 def mutation(child): for point in range(DNA_SIZE): if np.random.rand()< MUTATION_RATE: if child[point] == 1: child[point] = 0 else: child[point]=1 return child if __name__ == "__main__": #pop(population)为[0,2),popsize个,每个长为dnasize的随机数矩阵 #换言之,即由0,1组成的dna长链,种群中每个个体都不相同。 pop = np.random.randint(2,size=(POP_SIZE, DNA_SIZE)) plt.ion() x=np.linspace(*X_BOUND,200) plt.plot(x,F(x)) for flag in range(GENERATIONS): F_value = F(translateDNA(pop)) if 'sca' in globals(): sca.remove() sca = plt.scatter(translateDNA(pop), F_value, s=100,lw=0 , c='red',alpha=0.5);plt.pause(0.01) fitness = get_figness(F_value) pop = select(pop,fitness) pop_copy=pop.copy() #为产生子代而人为备份亲本 pop1 = pop for parent in pop: child = crossover(parent,pop_copy) child = mutation(child) parent[:] = child #完整复制一遍,同时改变了pop本身。 print('\r',flag,"/",GENERATIONS,end='', flush=True) print('\n',child) print(translateDNA(pop)) plt.ioff(); plt.show()结果如图所示:
遗传算法学习笔记一:重新发明简易轮子 想起高中,不妨回忆一下生物必修二在记忆中所占的权重。想一想刷遗传题时的痛苦和折磨,想一想减数分裂的框图有多长,生物老师让你默写过多少次减数分裂框图,最后生物必修二内容又能拿多少分。但这些可以是一个有趣的数学问题。为了让一个实际问题变得更容易贴合生物学实际,咱们先从二维函数极值点问题出发,去初步感受一下轮子是怎么变圆的。摘抄自百度百科:“遗传算法(Genetic Algorithm,GA)最早是由美国的 John holland于20世纪70年代提出,该算法是根据大自然中生物体进化规律而设计提出的。是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。该算法通过数学的方式,利用计算机仿真运算,将问题的求解过程转换成类似生物进化中的染色体基因的交叉、变异等过程。”对于遗传算法,核心有如下几个:1、figness适应度函数2、select选择3、crossover交叉4、mutantion变异这些概念可以十分轻松的在高中生物必修二中发现。这次我们将通过计算机方法去实现这个神奇的过程。因为站在如今人类的知识层级上,遗传算法塑造了我们,还让我们发现了遗传算法。其实我也不太记得人类是不是有丝分裂了,但是减数分裂还是记得的。但无论是何种分裂,核心是生物体的遗传信息存在与DNA中,DNA是携带遗传信息的长链,由四种碱基的不同排列组成了构成了纷繁复杂的生物体,以及他们各自的功能。没有DNA的此种特性,Shakespeare就无法love, write, sigh, pray, sue, and groan。也许DNA是图灵完备的,但是人类已经掌握二进制了,只需要两个数字即可构建如今的数字帝国。因此,进行遗传算法的第一项,就是将待求量二进制化。DNA = np.random.randint(2,size=(DNA_SIZE))此方法可以构建出由0,1组成,长为DNA_SIZE的表征二进制的数组。对于一定数量的种群,对每个种群个体分配DNA序列:#pop(population)为[0,2),popsize个,每个长为dnasize的随机数矩阵 #换言之,即由0,1组成的dna长链,种群中每个个体都不相同。 pop = np.random.randint(2,size=(POP_SIZE, DNA_SIZE)) 对于一个二进制数,它均可对应唯一一个十进制整数。由于用二进制非浮点数表示一个非整数数复杂的。因此我们可以采用一种比例放缩的方法。对于一个八位二进制数,可以对应0-255此256个十进制整数。将此256个数归一化再乘上目标求解区间长度。就可以得到具备一定精确度的取值空间了。这个过程可以看作转译过程,算法为:def translateDNA(pop): return pop.dot(2**np.arange(DNA_SIZE)[::-1])/float(2**DNA_SIZE-1)*X_BOUND[1] 其中,X_BOUND=[0,5]接下来,就可以放心构建算法核心了!对于要求解极大值的函数:def F(x): return np.sin(x)*5*x + np.cos(6*x)+1 构建与之相关的fitness适应函数:def get_figness(Y_values): return Y_values + 1e-5 - np.min(Y_values) # y_i值-所有y构成数组的最小值+定义的无穷小量 #遗传算法中不能出现负数,所以要加上无穷小量这个适应函数表征了某个体与最小适应性个体的差值。由于该问题是极大值问题,因此越大越好。Fitness的值可以表征选择该个体的适应性优劣,并可以在Select选择运算内作为选择个体的概率Select选择:在该环节内,要依据适应性能挑选出较优个体,模拟自然选择过程。将fitness的值传入该模块作为每个个体的选择权重。def select(pop,fitness): #注意random.choice函数:依据概率p在指定数组中选择在指定的数组中随机采样 idx = np.random.choice(np.arange(POP_SIZE),size= POP_SIZE,replace=True, p=fitness/fitness.sum()) return pop[idx] #随机选择种群中都某一个个体,表征个体的是他的dna 选择出来的大概率是适应性高个体,小概率是适应性个体。一时的失败不算是失败,运气也是实力的一部分也许。Crossover交叉环节:实际生物体遗传时,染色体见会发生交叉互换的情况。这里我们简化这种交叉互换,采用随机数的方式随机选择亲本处需要替换的地方。将亲本1的部分序列值由序列2对应部分替换,形成子代。这里用到的算法比较有意思,运用了bool类型在数组中的选择作用。首先我们生产与DNA等长的随机序列,并将其转换为bool类型:cross_points = np.random.randint(0,2,DNA_SIZE).astype(np.bool_) 输出形式为:[ True True False False False False True True False True]对于数组a而言,a[crossover_point]选择了所有bool类型为true的元素;而b[c_p]=a[c_p]就是将a中true的元素赋予b中true元素对应的位置上。进而完成交叉这一行为。def crossover(parent, pop): if np.random.rand()<CROSS_RATE: index = np.random.randint(0,POP_SIZE,size=1) cross_points = np.random.randint(0,2,DNA_SIZE).astype(np.bool_) #corssover的原理是由于cross_point被定义为了布尔类型: #对于数组a而言,a[crossover_point]选择了所有bool类型为true的元素 #b[c_p]=a[c_p]就是将a中true的元素赋予b中true元素对应的位置上。完成交叉。 parent[cross_points]= pop[index, cross_points] return parent mutation 变异:学核科学的,自然知道在辐射条件下基因会发生突变。因此,基因可能会发生良性突变,也可能发生恶性突变,但是总会有几率突变。定义突变机率:MUTATION_RATE = 0.003 def mutation(child): for point in range(DNA_SIZE): if np.random.rand()< MUTATION_RATE: if child[point] == 1: child[point] = 0 else: child[point]=1 return child (注意结合主循环内内容,之后会展示,此时,child已经变成一个体了)到此为止,我们已经得到了构成一个普通遗传算法的几个关键函数。接下来构建主函数,连接起各核心功能;流程图如下,图片抄自百度百科:定义种群生长代数:GENERATIONS=200对于每代种群:1、获取目标函数值:F_value = F(translateDNA(pop))2、获取个体适应度fitness = get_figness(F_value)3、Select选择:依据适应度选择多个个体并填充全部种群pop = select(pop,fitness)创建另一个亲本,采用复制的方式pop_copy=pop.copy()4、对于每一个个体与其另一亲本进行crossover交叉配对,且随之变异for parent in pop: child = crossover(parent,pop_copy) child = mutation(child) parent[:] = child #完整复制一遍,同时更改了pop本身 完整代码如下:import numpy as np import matplotlib.pyplot as plt DNA_SIZE = 20 X_BOUND=[0,5] POP_SIZE = 10 CROSS_RATE= 0.8 MUTATION_RATE = 0.003 GENERATIONS = 200 #GA作用的目标函数 def F(x): return np.sin(x)*5*x + np.cos(6*x)+1 #GA的核心:fitness适应度,评价子代的指标。 def get_figness(Y_values): return Y_values + 1e-5 - np.min(Y_values) # y_i值-所有y构成数组的最小值+定义的无穷小量 #遗传算法中不能出现负数 #在范围内将x编码成二进制数,并且将二进制数缩放到所需要的范围内。 #pop(population)是一个储存二进制DNA的矩阵,形状与POP_SIZE和DNA_SIZE相关。 #pop.dot(2**xxx)的部分实际上是利用数权法进行2-10进制转换;.dot是返回两个向量内积 def translateDNA(pop): return pop.dot(2**np.arange(DNA_SIZE)[::-1])/float(2**DNA_SIZE-1)*X_BOUND[1] ''' 进化的三要素:选择:select;交叉:crossover;变异:mutation ''' #第一步,选择 def select(pop,fitness): #注意random.choice函数:依据概率p在指定数组中选择在指定的数组中随机采样 idx = np.random.choice(np.arange(POP_SIZE),size= POP_SIZE,replace=True, p=fitness/fitness.sum()) return pop[idx] #随机选择种群中某一类个体并替换全部个体,选择后种群内个体几乎是适应性强的,表征个体的是他的dna #第二步,交叉配对 def crossover(parent, pop): if np.random.rand()<CROSS_RATE: index = np.random.randint(0,POP_SIZE,size=1) cross_points = np.random.randint(0,2,DNA_SIZE).astype(np.bool_) #corssover的原理是由于cross_point被定义为了布尔类型: #对于数组a而言,a[crossover_point]选择了所有bool类型为true的元素 #b[c_p]=a[c_p]就是将a中true的元素赋予b中true元素对应的位置上。完成交叉。 parent[cross_points]= pop[index, cross_points] return parent #第三步,变异 #child在主循环里已经定义为pop内的某一个体,因此只需要考虑dna上有多少基因需要突变即可。 def mutation(child): for point in range(DNA_SIZE): if np.random.rand()< MUTATION_RATE: if child[point] == 1: child[point] = 0 else: child[point]=1 return child if __name__ == "__main__": #pop(population)为[0,2),popsize个,每个长为dnasize的随机数矩阵 #换言之,即由0,1组成的dna长链,种群中每个个体都不相同。 pop = np.random.randint(2,size=(POP_SIZE, DNA_SIZE)) plt.ion() x=np.linspace(*X_BOUND,200) plt.plot(x,F(x)) for flag in range(GENERATIONS): F_value = F(translateDNA(pop)) if 'sca' in globals(): sca.remove() sca = plt.scatter(translateDNA(pop), F_value, s=100,lw=0 , c='red',alpha=0.5);plt.pause(0.01) fitness = get_figness(F_value) pop = select(pop,fitness) pop_copy=pop.copy() #为产生子代而人为备份亲本 pop1 = pop for parent in pop: child = crossover(parent,pop_copy) child = mutation(child) parent[:] = child #完整复制一遍,同时改变了pop本身。 print('\r',flag,"/",GENERATIONS,end='', flush=True) print('\n',child) print(translateDNA(pop)) plt.ioff(); plt.show()结果如图所示: